2021年6月26日土曜日

変異株の置き換わりについて

感染力の異なる複数の株があるときの感染者数の時間変化について考えたい。 特段の人為的な介入が行われず、なすがままに感染が広がっているとするとき、感受性のある (susceptible) 者の有限性を考える必要がない程度に感染が少数なら、株 $i$ の感染者数 $x_i\;(> 0)$ の時間変化は株に固有の定数 $k_i\;(> 0)$ を用いて、

$$\frac{\mathrm{d}x_i}{\mathrm{d}t} = k_i x_i \quad\tag{1}$$

で表されるだろう。 すなわち、この株の感染者数の時間に関する動きは指数関数 $x_i = A_i \exp(k_i t)$ で表される（ただし $A_i > 0$ は $t = 0$ における感染者数）。 $k_i$ が大きな株ほど広がりは速く $k_i$ は感染力を表すとみなせる。

広く他人との接触を抑制するような社会的な介入政策一般や（日本ではあまり有効に行われていない）防疫目的の検査による感染者数の時間変化に対する感染抑制の効果は、$k_i$ と同様に概ね感染者数に比例して作用するとみなせる。 その大きさは時間に関して変動するものの、株の種類には概ね依存しないと考えられる。 この影響を $c(t)$ と書けば、微分方程式 (1) は、

$$\frac{\mathrm{d}x_i}{\mathrm{d}t} = (k_i\!-\!c(t))\,x_i \quad\tag{2}$$

と変更される。 ワクチンの効果は株により抑制効果にある程度の違いがあるかもしれないが、その効果に時間による変動はないと考えられるので、（定数分の違いは無視して）同様に $c(t)$ に繰り込まれるものとする。 よって、このとき感染者数は、

$$x_i = \frac{A_i \exp(k_i t)}{\exp(C(t))} \quad\tag{3}$$

のように表される。ただし、$C(t) = \int_0^t c(\tau) \mathrm{d}\tau$ とした。 $C(t)$ は株に依存しない時間の関数と考えられたのであったから、複数の株 $i, j$ を考えるときその感染者数の比 $x_j/x_i$ を考えれば打ち消し合って、比は単純に人為的介入の効果に影響しない指数関数、

$$\frac{x_j}{x_i} = \exp((k_j\!-\!k_i)\,t) \quad\tag{4}$$

で表せることになると期待される。 ゲノム解析や特定の変異を検出する PCR 検査が無作為と見なせるように行われ市中の感染者数を反映しているなら、（サンプル誤差を除いて）(4) はそれら各株の感染確認者数においても成立する。

実際、2 変異株の比が概ね (4) の単純な関係に従っていることは図 1 でも実証される。 図 1 は東京都健康安全研究センターが週ごとに公表している PCR による変異株の変異検出数から作成したもので[1]、2021年3月以降に起こった第 4 波時の E484K 変異をもつ変異株から N501Y 変異をもつ変異株（後者は主に英ケントで最初に流行が確認された α 変異株）の比の時間変動を片対数グラフで示している。 比は、緊急事態宣言のような社会的介入の有無や感染確認者数の大小に影響を受けたようすはなく、(4) 式が示すように概ね直線で表される。 $k_{\,\mathrm{N501Y}}\!-\!k_{\,\mathrm{E484K}}$ に相当する傾きは 0.065 日−1 で、これら変異株それぞれの感染力の違いのみから定まる変異株間の移行の速さを表している。

図 1. 東京における E484K 変異をもつ変異株と N501Y 変異をもつ変異株の比（東京都健康安全研究センター調査[1]から）

一方、イギリスでは多くのゲノム解析を行って各都市の変異株の感染拡大状況を詳しく調べている。ロンドンにおける B.1.177+ 株（類似する株の集団）から α 株、および α 株から δ 株への置き換わりのようすを同様にプロットしてみると図 2 のようになる。

図 2. ロンドンにおける B.1.177+ 株（類似する株の集団）と α 株 (B.1.1.7)、および α 株と δ 株 (B.1.617.2) の比の時間変化（Wellcome Sanger Institute による lineage データ[2]から）

図 2 では、比の対数の時間変化は概ね直線に従うものの、途中からは反れてより緩やかな拡大となる傾向があるように見てとれる。 その理由は明らかではないが、地域的な人々のネットワークによる局所的な susceptible の有限性が効いているのかもしれない。 ただし、イギリスの数学者の Alex Selby 氏は Twitter 上で COG-UK (COVID-19 Genomics UK Consortium) のデータを用いたイギリスにおけるこの比が見事に指数関数に従うことを示している[3]。 Selby 氏は、イギリスにおける α 株から δ 株への置き換わりの傾き ($k_\delta\!-\!k_\alpha$) が安定して 0.11 日−1 であるとしている。 これは、以下で見る東京における δ 株への置き換わりの速さとおよそコンシステントである。

現在、首都圏および大阪などで進行中の α 変異株（B.1.1.7, イギリス株, ケント株）からより感染力の強い δ 変異株 （B.1.617.2, インド株）への置き換わりについて上の知見を具体的に当てはめてみたい。 しかし、それにはいくつかの困難がある。 日本においては、新型コロナのゲノム解析は感染研で行われているが、時間がかかる上にごく少数であり、報告は特定の都市別には公表されていない。 どのような株が存在するか絞られている場合には、代わりにそれぞれの変異株に特徴的な特定の変異（α 株の場合 N501Y, δ 株では L452R）を検出する自治体等による PCR 検査が参考となる。 しかし、一般には市中の変異株の割合を知るために重要な無作為抽出を考慮していない結果が報告されているようであり、これは特にクラスターが発生しそれらが変異検出の検査にかけられた場合、結果を歪ませることになる。 さらに検出された変異をもつ検体の数だけが報告され、いくつの検体を検査した結果なのか、サンプルサイズがわからない報告を行っている自治体も多いようだ。 また、最近の厚労省の指示により、主に α 株の数を知るために行われていた N501Y 変異検出のための検査を多くの自治体がやめてしまった。

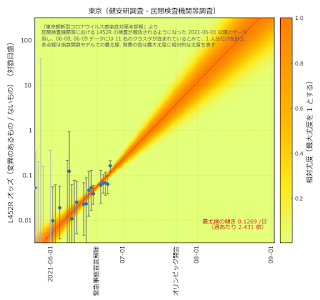
ここでは、少なくとも検査数を毎日公表している東京都の調査に基づいた分析のみを取り上げる。 東京都も N501Y の検査をやめ L452R の検査結果のみを公表しているので、δ 株（正確には L452R 変異を持つ株, 以下 δ 株と同一視する）以外の株はすべて α 株（同様に正確には N501Y 変異のある株）なのだと仮定する。 こととき求めるべき比は、δ 株の存在比 $p$ のオッズ $p/(1\!-\!p)$ ということになる。 東京都新型コロナウイルス感染症対策本部の本部報[4]を 2021 年 6 月 1 日から 25 日まで集計した結果は、図 3 左パネルのようになる。

図 3. 東京における L452R 変異をもつ株（主に δ 株）のオッズの対数（ロジット）とそれへの直線の当てはめ（左）. 同じものを割合で表したもの（右）.（東京都新型コロナウイルス感染症対策本部報[4]より）

図 3 でも概ね置き換わりが (4) で示される指数関数に従っていることがわかる。 ただし、用いているデータは本来、無作為抽出を意図したものではないため、偏りが存在すると思われる。 特に、クラスターが発生し、クラスターの集団に含まれる検体が複数変異の検査を受けた場合、結果を過大に評価することになる。 市中での δ 株の割合を知りたいというここでの目的においてはこれは不適切なため、図 3 では報道を元にクラスターが含まれると思われる結果は修正している。しかし、想定より上に飛び出しているものには依然こうした互いに関連した検体の結果が含まれているかもしれない。

なお技術的なこととして、図 3 は、扱っている範囲において依然置き換わりの初期であって δ 変異株の割合は小さい。 またサンプルサイズも小さな場合があるため、サンプル誤差を与える二項分布の歪が大きく、対数をとって最小二乗法で回帰直線を求めることはあまり適切ではないと思われる。 このため、二項分布の歪はなるべく保ったままモデルの直線を与えるパラメーター空間を網羅的に走査してそれらの尤度を求めている。 ここでは、これらの手続きの数学的詳細は省く。

この結果を用いると、変異株の割合の今後の変化だけでなく、感染者数のある程度の予測を行うことができる。 これについては項を改めて論じる。

  • 2021-06-26: 図 1 を差し替えました。
  • 2021-06-28: 図 2 を差し替え、関連する記述を一部修正しました。
  • 2021-06-29: 一部推敲。
投稿者 時刻: 0 件のコメント:

2020年4月26日日曜日

観測された感染者数に関する覚書き 3

前記事で用いた $I_E(t\,;t_P)$ および $c_E(t\,;t_P)$ を、韓国・ドイツ・日本の 3 か国およびアメリカ・ニューヨーク州について示し、それぞれについて検討する。 データにはジョンズ・ホプキンズ大学 CSSE が公開している 2020 年 4 月 23 日までの時系列データを用いた（差分を取るため 4 月 22 日が $t_P$ となる）[1]。

韓国

韓国においては 2020 年 2 月 18 日に大邱（テグ）市で宗教団体に関係する感染者が見出だされ、翌 19 日に集団感染が発生していることが把握された。 その後、宗教団体に関係する者に関しては全数検査が行われた。 3 月 8 日の時点において、この集団感染による感染者が 4500 件近くあり、韓国の感染者の 6 割以上を占めていることが韓国における感染の特徴と言える[2]。 長期的に見れば、3 月後半以降、現在までに 2500 人程度の新たな感染者が見つかっており[1]、それもよく防がれているように見える。 しかし全体としてみれば発見の量は初期の動きに比べ小さい。 よって、これらはここに示した感染拡大初期に関して $I(t)$ および $c(t)$ の比較的よい近似を与えているものと思われる。

図に示されていない範囲で起こったと思われる大規模な集団感染時には、$I(t)$ の名目上の倍加時間は短かったといえるかもしれない。 しかし、それは飽くまで集団感染に起因するものである。 大邱での大規模な検査が始まった時点での観測された感染者数 $H(t)$（上図灰色の実線）の急激な上昇は多数の検査を行った帰結であり、隠れた感染者 $I(t)$ はその時点ですでに数千人いたとするのがもっともらしい。 仮にこの時期に感染自体の倍加時間 $D$ が 2-3 日のように短かい期間で拡大したのだとしても、上図のように検査と隔離の効果で増加は抑えられており、後に徐々に減少したのではないかと思われる。 実際には、初期の隠れた感染者 $I_0$ がもっと多く、$D$ がもっと長かったとして矛盾はない。 初期の韓国においては限定された集団を無症状者も含めて網羅的に検査できたことが、その後の $I(t)$ の減少に大きく寄与したと考える。 徹底した早期の検査がその後の感染拡大をうまく喰い止めた例は、規模は異なるが日本の和歌山県における病院での集団発生後の状況も事例として挙げられるだろう。

検査率を上から抑える $c_E(t\,;t_P)$ のグラフは概ね高い値を示し、倍加時間が長い場合も、初期の検査で隠れた感染者を 1 日あたり数 % のオーダーで見つけ出していたものと思われる。 $I_0$ の見積もりと合わせれば、最初の記事で述べた $A = c I_0$ はオーダーとして初期に 100 人/日程度であったろう。 例として、大邱の集団感染発覚当初からしばらくたった状況を考え、$H^* = 1000$ 人とすれば、2 月 25-26 日にこの基準を超える。 一方、2 月 23-28 日の見かけの累積確定例時定数は約 3.7 日（倍加時間約 2.6 日）の依然として短いものであった。 これより仮に $A/H^* \approx 0.1$ として、$d(\log \tilde{H})/dt = \lambda + A/H^*$ の関係を用いれば、実際の時定数は $1/\lambda \approx 6$ 日（倍加時間約 4 日）となり、検査によるの見かけの効果が実際に働いていたであろうことが裏付けられる。

ドイツ

ドイツで本格的に検査が拡大したのは 2020 年 2 月 26 日頃だが、政府が拘束力のあるロックダウンの措置を行ったのは 3 月 23 日だった[3]。 検査数は 3 月半ば頃より拡大され、1 日あたり 5 万件の大規模な検査が行われてきた[4]。 3 月下旬からは無症状者への検査も行われた[3]。 観測された感染者数（累積確定例）は、3 月中旬ごろまでおおむね倍加時間 3 日ほどであった。

極端に短くない倍加時間 ($D \geq 4$) を考えたとき、グラフから、ドイツにおいて観測された累積の感染者数 $H(t)$（灰色）が隠れた感染者数の下限 $I_E(t\,;t_P)$（実線）を超えたのは、ロックダウンが発令された 3 月下旬に入ってからであることがわかる。 すなわち、そのころには少なくともまだ把握された感染者と同等以上の隠れた感染者がいたことになる。 仮に、3 月 18 日時点で、観測された感染者の 5 倍の隠れた感染者がいたとしたとき、一定の倍加時間のもとそれ以前の感染者数がどのようであったかを破線で表している。 前出の $I_R$ に相当するこの追加の感染者は単純に指数関数的に増大するので、この程度の大きさであった場合、下限 $I_E$ との初期の比はずっと小さくなる。 よって、これらの時点で韓国ほどには初期換算感染者を削りきれていないであろうドイツにおいても、検査初期の 2 月 25 日に数千程度の隠れた感染者がいたとすれば、見かけと異なって倍加時間 4 日以上で拡大していたとして矛盾はない。

検査率の最大値 $c_E$ は、3 月初めごろまでは韓国より小さな値を示しており、長い倍加時間を想定した場合、1 日 1 % に満たないものだった。 よって、$A$ の効果もこのころには韓国より 1 桁ほど小さかったかもしれない。 その後、$c_E$ は急激に上昇しており、実際の検査率も同様の傾向があったと思われる。 このことは、ドイツの初期の倍加時間が韓国ほど短くなかったことを説明するかもしれない。

初期の倍加時間を 6 日とした場合、ロックダウン宣言の 3 月 23 日までに削った初期換算感染者数 $J(t)$（起点 2 月 26 日）は約 3100 人、倍加時間 3 日とした場合、約 490 人である（前記事の図参照）。 これは、広範な検査と隔離とが行われなかった場合、3 月 23 日までの 26 日間で、それぞれ約 6 万 2 千人と約 20 万人に拡大したはずのものとなり、判明した感染者の隔離が適切に行われているなら大規模な検査には隠れた感染者の削減に大きな効果があったことがわかる。

ニューヨーク州

大規模な感染拡大がみられたニューヨークでは、最初の確定例が見つかった 2020 年 3 月 1 日（JHU CSSE データでカウントされたのは翌 2 日）以降、検査による累積確定例の急激な上昇が見られた。 3 月 5-19 日の見かけの倍加時間は 1.8 日であった。 一方、2020 年 4 月 23 日のニューヨーク・タイムズは、3 月 1 日の時点で実際には（ニューヨーク市のみで）1 万人を超える隠れた感染者がいたのだとするノースイースタン大学の研究グループの研究を紹介している[5]。 4 月 25 日現在、研究の詳細は明らかでないが、この値は倍加時間がある程度長いとした場合の隠れた感染者の最小値 $I_E$ と矛盾しない。 図では $I_E$ が 1 万より小さい倍加時間 6 日以下の場合に関して、3 月 1 日の時点で 1 万人の隠れた感染者がいたとした場合のその後の隠れた感染者数を破線で示している。

日本

観測された感染者数 $H(t)$ や、それによる初期換算感染者数 $J(t)$ で特異的な少なさを示している日本においては、$I_E$ および $c_E$ のグラフも特異的なものとなっている。 パラメーターの倍加時間にあまり依存せず、隠れた感染者の最小値 $I_E$ は $H(t)$ に沿って増加し、検査率の最大値 $c_E$ は時間に依存しない大きな一定の値を示している。 検査の強い抑制によって、これらは実際の値と大きく離れたものでありうる。 しかし、検査の強い抑制が一定の基準で行われ続けていると考えるなら、$c(t)$ がほぼ定数となることと、$H(t)$ のほぼ一定の時定数が隠れた感染者 $I(t)$ のそれを反映していることとは想定しうるだろう。

2 月 15 日から 30 日間の倍加時間はおよそ 7 日であり、これが初期の $I(t)$ の倍加時間も反映していると思われる。 このときの $I_0$ の最小値、すなわち検査が削った初期換算感染者数は 240 人程であるが、4 月下旬も隠れた感染者が少なからず存在していることを考えれば、起点とした 2 月 14 日の感染者はこれよりはるかに多かった。 図では、$I_0$ が 1000 人とした場合と 10000 人とした場合のその後の動きを破線で示している。 隠れた感染者は検査からほとんど影響を受けることなく、ほぼ指数関数的に増大する。 倍加時間 7 日が続いていたとした場合、これらの $I_0$ による 4 月 1 日（47 日後）の隠れた感染者数は、それぞれ約 8 万 6 千人と、約 103 万人となる。

*   *   *

結局、観測された感染者数の動きを隠れた感染者数と正しく区別して論じるならば、日本の観測された感染者数の少なさを、日本の隠れた感染者数がヨーロッパ諸国で想定される値よりもずっと小さいとする根拠とすることはできないことがわかる。

「新型コロナウイルス感染症対策専門家会議」は2020 年 4 月 1 日の資料においていわゆる「オーバーシュート」に関し「我が国では、今のところ諸外国のような、オーバーシュート（爆発的患者急増）は見られていない」として、次のような注釈を加えた[6]。

オーバーシュート： 欧米で見られるように、爆発的な患者数の増加のことを指すが、2～3 日で累積患者数が倍増する程度のスピードが継続して認められるものを指す。異常なスピードでの患者数増加が見込まれるため、一定期間の不要不急の外出自粛や移動の制限（いわゆるロックダウンに類する措置）を含む速やかな対策を必要とする。（後略）
さらに太字とアンダーラインで強調し、
いわゆる「医療崩壊」は、オーバーシュートが生じてから起こるものと解される向きもある。しかし、新規感染者数が急増し、クラスター感染が頻繁に報告されている現状を考えれば、爆発的感染が起こる前に医療供給体制の限度を超える負担がかかり医療現場が機能不全に陥ることが予想される。
とした。

すなわち専門家会議によれば「オーバーシュート」は「欧米」で見られたような単に倍加時間 2-3 日の継続的拡大を意味するとし、このような短い倍加時間による増大がなくとも、医療のリソース不足による機能不全が迫っていることに警鐘を鳴らした。 しかし、この小論で明らかとしたように、ヨーロッパ諸国やアメリカの都市で初期に見られたこのような短い倍加時間の「爆発的急増」は大規模な検査を行うことによってすでにいた隠れた感染者を発掘した見かけの効果だろう。 日本が検査数を絞っているが故に、日本においてはそのような増加は見えず、逆に日本でも諸外国でもそれよりはやや長い一定の倍加時間での指数関数的拡大を継続的に続けている。 この点で日本の状況は何ら諸外国と変わる点を見出だせない。 違いは、日本の倍加時間が幸いにもヨーロッパなどよりやや長いと思われることと、逆に日本がほとんど検査を行っていないために感染者を適切に削っていくことができなかったことである。 指数関数的拡大を続ける限り、倍加時間の多少の長短にかかわりなく医療崩壊のような同等の帰結がもたらされるのは当然である。

「オーバーシュート」(overshoot) の語は、本来、なにがしかの量に対して、他の要因から想定したなにがしかの基準が先にあり、実際の量がそれを超えていくことを表すのに相応しい語である。 そうした他の要因が見えない「爆発的急増」もしくは「倍加時間 2-3 日」を単に表すとした用法は甚だ奇妙にみえる。 ここからは想像であるが、むしろその基準は上の言と逆に専門家会議こそが医療崩壊を想定していたのではないか。 倍加時間 2-3 日という事態が実在のものと思い込み、そのような事態になれば否応なくすぐさま医療崩壊に至ると考えたとするならば、「オーバーシュート」という語を用いた意味が理解できる。 実際には、そのような増加がなくとも隠れた感染者数は長めの倍加時間での指数関数的増大を続け、医療崩壊が想定される状況まで至ったために、医療崩壊と関係しない「オーバーシュート」＝「爆発的増加」という本来の語の意味と合わない置き換えが成立したのではないだろうか。 もしそうだとすれば、専門家会議は自らが立てた不適切な道標によって自ら勝手に道を誤っていることとなる。

投稿者 時刻: 0 件のコメント:

2020年4月18日土曜日

観測された感染者数に関する覚書き 2

（2020 年 4 月 25 日に改稿し、実データを用いた解析は後続の別記事としました）

再掲した下図からも明らかなように、疫病を終息させることは隠れた感染者 $I$ を消滅させることであり、そのためには $I$ を増加させる感染率 $a$ を減らすか、$I$ を減少させる検査・隔離率 $c$ を増やすかする以外にない（自然の回復率 $b$ を人為で変えることは難しいだろう）。 ロックダウンや社会的距離を保つといった政策は $a$ を減らすことに該当し、広範な検査を行うことは $c$ を増やすことに当たる。 この両面作戦のうち、日本は $c$ を増やすという手段をほとんど採ることなく、結果として $I$ の大きさも推測し難いものとなっている。


疫病の終息は、$a$ を減らし $c$ を増やすことで $a - b - c < 0$ に持ち込むことが前提となる。

感染率 $a$ と検査率 $c$ を推測する何らかの方法なしには観測された感染者数（われわれが感染者数として把握しているもの）である $H$ から、隠れた感染者数 $I$ を推測する方法はあまりない。 特に少ない $H$ しか捉えていない日本ではそうだろう。 ただしわずかながら（ある仮定のもとで）、$H$ の増分の時系列データから、検査によってどの程度の潜在的な感染を防いできたのかを推定でき、そこから $I$ を下から抑える（それよりも小さくはないと言える値を求める）ことはできると思われる。 これによって特に、検査開始時にいたであろう隠れた感染者数 ($I_0$) とそのときの検査率（$c(0)$: 単位時間あたりに隠れた感染者のうちどれだけの割合を検査で捉えたか）に対するおおよその見積もりが与えられる。

*   *   *

少なくとも感染率 $a$ を減少させるような強力な政策が行われなかった初期において、$a$ （および $b$）を一定とみなすことができるとする（$c$ は時間の関数とする）。 このとき、前の記事のように、隠れた感染者数 $I(t)$ と観測された（検査・隔離された）感染者数 $H(t)$ の時間変化は、それらが人口に比べまだ小さいとき、 $$\dot{I}(t) = (a - b - c(t)) I(t), \quad \dot{H}(t) = c(t) I(t)$$ と見ることができる（ただし、時間微分を上付きのドットで表した）。 $\dot{H}(t)$ は、われわれが（少なくとも日ごとの差分として）知ることができる値であり、$a, b$ はパラメーターとして仮定される。 これらから、 $$\dot{I}(t) = (a - b) I(t) - \dot{H}(t)$$ よって、$I(t)$ は、 $$I(t) = \left(I_0 - \int_0^t \dot{H}(u)\,e^{-(a - b) u} du\right) e^{(a - b) t}$$ となる。

上式に含まれる積分、 $$J(t) = \int_0^t \dot{H}(u)\,e^{-(a - b) u} du$$ は、検査によって隔離された感染者数を $t = 0$ 時点に換算した人数だとみることができる。 この $J(t)$ を（$t$ までに観測された感染者の）「初期換算感染者数」と呼ぶこととする。

より詳しく言えば、時刻 $t = 0$ における感染者 1 人は隔離がなされなかったとき、時刻 $t$ で $e^{(a - b) t}$ に膨らみ、逆に $t$ における感染者 $h$ 人は、$t = 0$ において $h e^{- (a - b) t}$ 人から広まったと考えられる。 $h$ が各時点での検査を経た時間あたりの隔離者 $\dot{H}(t)$ であれば、$J(t)$ は時刻 $t$ までの検査・隔離者が $t = 0$ において何人であったかに換算した人数である。

$a$ と $b$ が一定というここでの仮定のもとで、時刻 $t$ においても隠れた感染者であり続ける集団の数は、$I_0$ から $J(t)$ を除いた残りの人々が拡大したものと捉えられ、上式、 $$I(t) = (I_0 - J(t))\,e^{(a - b)t}$$ が確かめられる。 ここでのように感染者数を初期時刻 $t = 0$ に換算して眺めるなら、検査による感染者の発見と隔離とは、$I_0$ から感染者を削っていく作業だと見ることができ、上の因子 $I_0 - J(t)$ は時刻 $t$ までにそれが削られた残りの量を表している[1]。 そして他方の因子 $e^{(a - b)t}$ が示すように、その作業は時間が経つほど指数関数的に困難なものとなる。 すなわち、感染拡大防止のためには初期に広範な検査を行うことが極めて有効であることを意味する。

*   *   *

$a - b$ または倍加時間 $D = \ln 2/(a - b)$ の値を仮定すれば、日々公表されている国や地域別の観測された確定者の人数によって $J(t)$ を評価できる。 以下の表は、ジョンズ・ホプキンズ大学 CSSE の確定者時系列データに基づきドイツ、イタリア、韓国、日本の 4 か国に関してこの換算人数を求めたものである（2020 年 4 月 15 日までのデータに基づく）。 なお、$t = 0$ となる起点にはそれぞれの国で検査がある程度まとまって行われ出した日を取っている。 また、図は $t$ に関する $J(t)$ の変化を通常のグラフと片対数グラフで表す。 起点として取った時刻から時間が経過すれば、検査による $J(t)$ の上昇は相対的に小さなものとなっていく。

検査・隔離により除かれた初期換算感染者数 $J(t)$
起点D = 3 日D = 5 日D = 7 日
ドイツ2020-02-26527 人2966 人7589 人
イタリア2020-02-211007 人4128 人9551 人
韓国2020-02-201134 人2207 人3119 人
日本2020-02-1548 人111 人218 人

韓国を除く各国で 4 月 15 日現在、まだ隠れた感染者が多く残っていると思われることを考えるなら、初期の感染者 $I_0$ はこれらの数字よりも大きなものであった。 また日本においては特異的に、検査人数が隠れた感染者の削減に直接寄与していないだろうことがここからも見て取れる。 日本と他国との比は 10 倍を超えるものとなっており、初期感染者数 $I_0$ がそれぞれの国で同等であったとするなら、これは観測された感染者が隠れた感染者よりも大きく下回っているであろうことを示唆する。

*   *   *

上で検査で感染者を見つけることは、初期換算感染者に換算するとき、検査開始時に市中あった隠れた感染者 $I_0$ を削っていく作業であると捉えられることを見た。 しかし、$I_0$ そのものは不明であり、ひいては隠れた感染者 $I(t)$ がどこまで拡がっているのかも一般に直接知ることはできない。 ただし感染が終息したなら、事後的に推測できる。 仮に時刻 $t^*$ において隠れた感染者 $I(t^*)$ を 0 にできた（終息した）とする。 このとき、$J(t^*) = I_0$、すなわち検査による初期換算感染者数が $I_0$ をすべて削ったこととなり、過去の $I(t)$ の動きは、 $$I(t) = (J(t^*) - J(t))\,e^{(a - b) t}$$ として表される。

現在時刻 $t_P$ が終息以前 $t_P \leq t^*$ の場合、過去の時刻 $t$ $(0 \leq t \leq t_P)$ における隠れた感染者 $I(t)$ は部分的にのみ判明しており、それを初期換算した感染者数 $I_0 - J(t)$ は未知の部分と既知の部分に分けられる。 $I_0 - J(t_P)$（上図ピンク色部分）は、現在時刻 $t_P$ における隠れた感染者 $I(t_P)$ に相当する部分であり、依然その大きさを定められないが、$I_0 - J(t_P)$ は $t$ によらず、自然な感染拡大の時定数 $1/(a - b)$ で単純に指数関数的に拡大する。 これを $I_P(t\,;t_P)$ と記せば、 $$I_P(t\,;t_P) = (I_0 - J(t_P))\,e^{(a - b) t} \qquad (0 \leq t \leq t_P)$$ となる。 一方、$J(t_P) - J(t)$（上図緑色部分）は $t$ により変化し、時刻 $t$ 以後 $t_P$ までに削られた隠れた感染者に対応する部分である。 これを、 $$I_E(t\,;t_P) = (J(t_P) - J(t))\,e^{(a - b) t} \qquad (0 \leq t \leq t_P)$$ と表すものとする。 これは、$t_P$ までに判明している $J(t)$ によって求められる既知の部分となり、$I(t)$ を下から抑える。

$J(t)$ は $t$ に関して単調増加するので、$I_E(t\,;t^\prime_P)$ は $t^\prime_P$ に関して単調増加となる（すなわち、$t_{P1} \leq t_{P2} \Rightarrow$ 任意の $t < t_{P1}$ に関し $I_E(t\,; t_{P1}) \leq I_E(t\,; t_{P2})$）。 よって、特にその時点で最新となる時刻 $t_P$ の $I_E(t\,;t_P)$ が $t$ に関して最良の（最も大きな）ものとなる。

また、$I_E(t\,;t_P)$ を用い、$\dot{H}(t) = c(t) I(t), \; I_E(t\,;t_E) \geq 0$ から、検査率 $c(t)$ を上から抑える関数、 $$c_E(t\,;t_P) = \frac{\dot{H}(t)}{I_E(t\,;t_P)} \quad (\geq c(t)) \qquad (0 \leq t \leq t_P)$$ を考えることができる。

ここでは感染率 $a$ を一定のパラメーターとしているが、実際には多くの国で漸次、感染率 $a$ を減らす多大な努力が行われている。 また現時点では隠れた感染者数が十分少なくなったと見なせる国は少ない。 これらを考えるなら、ここでの $I_E(t\,;t_P)$ はよい下限を与えているとは言えない。 特に、日本のような検査を強く制限してきた国に関しては、実際の隠れた感染者数と大きな乖離が見込まれる。 一方、比較的早期に隠れた感染者を $0$ に近い値に抑え込めた韓国のような国に関しては、$I(t)$ およびそれと $H(t)$ との関係、あるいは感染初期における実際の感染率 $a$ や検査初期の隠れた感染者数 $I_0$ を考えるヒントを与えるかもしれない。 次記事において、いくつかの国に関して 2020 年 4 月 15 日時点を $t_E$ とし、倍加時間 $D = \ln 2/(a - b)$ を 1 から 9 まで変化させた $I_E(t\,;t_P)$ と $c_E(t\,;t_P)$ を求め、それらの含意について特に感染拡大初期に関し検討する。

  • [1] @barlow2001 tweet on 2020-04-23. ご精読とご指摘に感謝します。
投稿者 時刻: 0 件のコメント: