ただいま 28 輪開花中

写真だと色が変わってしまう。

Bjarne 的なるもの

なんとなく first, last だのの algorithm 関数のインターフェースが好きになれなくて、せいぜい vector<T> をベター配列ぐらいでしか使ったことなかったけれど、今頃になって STL で真面目に遊ぶ。 C++0x? Boost? 何それうまいの?

For each 的なるものに ruby とかでブロック (ruby の用語だとイテレータ?) を渡すのに比べて、関数オブジェクトとかはクラスを宣言しなければいけないしめんどくさいなあ的なるものかと思ってたけど、その分、抽象的な処理が何か考える契機にはなるのかな。 ∀x/∃x の関数オブジェクト・ラッパーをさんざ設計してみた後で、それじゃ短絡評価されないじゃんということにやっと気づく連休初日。 なるほど find_if() とか adjacent_find() を使えと。 0x だと無名のラムダ関数的なるものを関数定義中に書けるようになるとか…。 これ以上文法を複雑にしないで。

ファンクショナル (汎関数) はまだしも関数オブジェクトをファンクター (関手) とか呼んでるのがあるのは何か違う気がする。 そういう文脈があるのだろうか。 むしろ for_each() とかの方がファンクター的なるものっぽいのだけれど。 for_each(first, last, f) の代わりに g = for_each(f); g(first, last); とかだともっといいか。 まったく需要なさそうだ。

コンテナの実体の代わりにインデックスをソートしてみるとかに使えそうな関数オブジェクト・ラッパー↓。 長たらしい。 筋は通ってるけど多重継承で同じクラスを継承する極悪っぷりなので、親切なコンパイラのウォーニングは無視する。 なんかこれも別の手段がありそうだ。

#include <functional>
#include <iterator>

// 単項関数ラッパー基底クラス
// 他のラッパー・クラスの基底となり、ラップされる関数オブジェクトを保持する
//  関数オブジェクトの呼び出し  (*this)(-): A → R
// テンプレート引数
//  A   呼び出しと F の引数型               要件 なし
//  R   呼び出しと F の返り値型 (void 可)   要件 なし
//  F   ラップされる関数の型                要件 -(-): F×A → R
//
template<typename A, typename R, typename F>
class  unary_function_wrapper_t  : public std::unary_function<A, R>
    {
    private:
        F  _wrapped_function;   // ラップされる非定数関数: 内部状態を持ち呼び出しで更新するかもしれない
        static R  _constraint_F(F f, A a)  throw ()  { return f(a); }
    public:
        explicit  unary_function_wrapper_t(F wrapped_function = F())  throw ()
            : _wrapped_function(wrapped_function) { R (* c)(F, A) = _constraint_F; }
        F const&  wrapped_function()  const throw ()  { return _wrapped_function; }
        R  operator()(A a)  { return _wrapped_function(a); }
    };

// 配列 (ランダム・アクセス・シーケンス) のインデックスを取って演算を行う
// コンストラクタの引数で A 型シーケンスのポインタまたはイテレータを与え、
// アルゴリズム関数にはその順番を示す I 型インデックスを与える
// 演算はシーケンス上の A 型の値に対して行われるが、
// アルゴリズム関数の操作はインデックスに対して行われる
//  関数オブジェクトの呼び出し  (*this)(-): I → R
// テンプレート引数
//  Aa  配列 (コンテナ) の先頭ポインタ (イテレータ) 要件 -[-]: Aa×I → A
//  R   呼び出しと F の返り値型 (void 可)           要件 なし
//  F   ラップされる関数 (オブジェクト) 型          要件 -(-): F×A → R (基底クラスより)
// 非明示型
//  A   F の引数型                                  要件 なし
//  I   呼び出しの引数型でインデックスとなる型      要件 なし
//
template<typename Aa, typename R, typename F>
class  unary_function_deindexer_t
    : public unary_function_wrapper_t<typename std::iterator_traits<Aa>::value_type, R, F>,
      public std::unary_function<typename std::iterator_traits<Aa>::difference_type, R> // 意図した多重継承
    {
    private:
        typedef typename std::iterator_traits<Aa>::value_type       A;
        typedef typename std::iterator_traits<Aa>::difference_type  I;
        Aa  _values_a;  // A 型配列 (コンテナ) への非定数ポインタ (イテレータ): このクラスの代入を可能にする
        static A  _constraint_Aa(Aa aa, I i)  throw ()  { return aa[i]; }
    public:
        explicit  unary_function_deindexer_t(Aa values_a, F wrapped_function = F())  throw ()
            : unary_function_wrapper_t(wrapped_function), _values_a(values_a)  { A (* c)(Aa, I) = _constraint_Aa; }
        Aa  values_a()  const throw ()  { return _values_a; }
        R  operator()(I i)  { return unary_function_wrapper_t::operator()(_values_a[i]); }
    };

// 2 項関数ラッパー基底クラス
//  関数オブジェクトの呼び出し  (*this)(-,-): A1×A2 → R
// テンプレート引数
//  A1  呼び出しと F の第 1 引数型          要件 なし
//  A2  呼び出しと F の第 2 引数型          要件 なし
//  R   呼び出しと F の返り値型 (void 可)   要件 なし
//  F   ラップされる関数の型                要件 -(-,-): F×A1×A2 → R
//
template<typename A1, typename A2, typename R, typename F>
class  binary_function_wrapper_t
    : public std::binary_function<A1, A2, R>
    {
    private:
        F  _wrapped_function;
        static R  _constraint_F(F f, A1 a1, A2 a2)  throw ()  { return f(a1, a2); }
    public:
        explicit  binary_function_wrapper_t(F wrapped_function = F())  throw ()
            : _wrapped_function(wrapped_function) { R (* c)(F, A1, A2) = _constraint_F; }
        F const&  wrapped_function()  const throw ()  { return _wrapped_function; }
        R  operator()(A1 a1, A2 a2)  { return _wrapped_function(a1, a2); }
    };

// 配列 (ランダム・アクセス・シーケンス) のインデックスを取って演算を行う
//  関数オブジェクトの呼び出し  (*this)(-,-): I×I → R
// テンプレート引数
//  Aa  配列の先頭ポインタ                      要件 -[-]: Aa×I → A
//  R   呼び出しと F の返り値型 (void 可)       要件 なし
//  F   ラップされる関数 (オブジェクト) 型      要件 -(-): F×A×A → R (基底クラスより)
// 非明示型
//  A   F の引数型                              要件 なし
//  I   呼び出しの引数型でインデックスとなる型  要件 なし
//
template<typename Aa, typename R, typename F>
class  binary_function_deindexer_t
    : public binary_function_wrapper_t<typename std::iterator_traits<Aa>::value_type,
                                       typename std::iterator_traits<Aa>::value_type, R, F>,
      public std::binary_function<typename std::iterator_traits<Aa>::value_type,
                                  typename std::iterator_traits<Aa>::value_type, R> // 意図した多重継承
    {
    private:
        typedef typename std::iterator_traits<Aa>::value_type       A;
        typedef typename std::iterator_traits<Aa>::difference_type  I;
        Aa  _values1_a;
        Aa  _values2_a;
        static A  _constraint_Aa(Aa aa, I i)  throw ()  { return aa[i]; }
    public:
        explicit  binary_function_deindexer_t(Aa values_a, F wrapped_function = F())  throw ()
            : binary_function_wrapper_t(wrapped_function), _values1_a(values_a), _values2_a(values_a)
            { A (* c)(Aa, I) = _constraint_Aa; }
        explicit  binary_function_deindexer_t(Aa values1_a, Aa values2_a, F wrapped_function = F())  throw ()
            : binary_function_wrapper_t(wrapped_function), _values1_a(values1_a), _values2_a(values2_a)
            { A (* c)(Aa, I) = _constraint_Aa; }
        Aa  values1_a()  const throw ()  { return _values1_a; }
        Aa  values2_a()  const throw ()  { return _values2_a; }
        R  operator()(I i1, I i2)  { return binary_function_wrapper_t::operator()(_values1_a[i1], _values2_a[i2]); }
    };

// 配列 (ランダム・アクセス・シーケンス) のインデックスを取って比較演算を行う
//  関数オブジェクトの呼び出し  (*this)(-,-): I×I → bool
// テンプレート引数
//  Aa  配列 (コンテナ) の先頭ポインタ (イテレータ) 要件 -[-]: Aa×I → A (基底クラスより)
//  F   ラップされる関数 (オブジェクト) 型          要件 -(-): F×A×A → bool (基底クラスより)
// 非明示型
//  A   F の引数型                                  要件 なし
//  I   呼び出しの引数型でインデックスとなる型      要件 なし
//
template<typename Aa, typename F>
class  comparator_deindexer_t
    : public binary_function_deindexer_t<Aa, bool, F>
    {
    public:
        explicit  comparator_deindexer_t(Aa values_a, F wrapped_comparator = F())  throw ()
            : binary_function_deindexer_t(values_a, wrapped_comparator) {}
        explicit  comparator_deindexer_t(Aa values1_a, Aa values2_a, F wrapped_comparator = F())  throw ()
            : binary_function_deindexer_t(values1_a, values2_a, wrapped_comparator) {}
    };

どういうときに使えそうかというと、例えば、うららかな春の陽気にさそわれて、ふと大量の数ベクトルを大きさの順にソートしたくなったとしよう。 ソートしたいのはベクトルなんだけど、比べたいのはその大きさ。 比較関数で比較の度にいちいち大きさを計算するのはばかばかしい。 そこで、大きさをあらかじめ計算した vector<double> を用意しておいて、0,1,2,...,n−1 に初期化したインデックス vector<size_t> も用意しておいて、比較関数は大きさの vector を参照させて、ソートはインデックスの vector に対して行う。 よくある手法だ (おそらく)。 STL でやると、大きさの代わりに絶対値の 2 乗をとる関数オブジェクトと、0,1,2,... を作るための関数オブジェクト、ついでに出力用関数オブジェクトを用意して：

#include <iostream>
#include <numeric>
#include <cstdlib>

template<typename Ka>
struct  sqabs_t  : public std::unary_function<Ka, typename Ka::value_type>
    {
        typedef typename Ka::value_type K;
        K  operator()(Ka const& ka)  { return std::inner_product(ka.begin(), ka.end(), ka.begin(), K()); }
    };

template<typename K, typename I = size_t>
class  counter_t  : public std::unary_function<K, I>
    {
    private:
        I  _count;
        static I  _constraint_I(I i)  throw ()  { return i ++; }
    public:
        explicit  counter_t(I initial_count = I())  throw ()  : _count(initial_count) { I (* c)(I) = _constraint_I; }
        I  count()  const throw ()  { return _count; }
        I  operator()(K const&)  throw ()  { return _count ++; }
    };

template<typename Ka>
struct  writer_t  : public std::unary_function<Ka, void>
    {
        typedef typename Ka::value_type K;
        void  operator()(Ka const& ka)  const
            {
                std::cout << "( ";
                std::copy(ka.begin(), ka.end(), std::ostream_iterator<K>(std::cout, " "));
                std::cout << ")\n";
            }
    };

そして、本体はこんな風になる：

#include <vector>

typedef double           Kt;
typedef std::vector<Kt>  Kat;
typedef std::vector<Kat> Kaat;
typedef size_t           It;
typedef std::vector<It>  Iat;

// ベクトルが入ったベクトルがあるとしよう
Kaat kaa;
for (size_t i = 0; i < 10; i ++) {
    Kat ka;
    ka.push_back(rand()); ka.push_back(rand()); ka.push_back(rand());
    kaa.push_back(ka);
}

//------

// 各ベクトルの絶対値の 2 乗のベクトルを用意する
Kat aa;  std::transform(kaa.begin(), kaa.end(), back_inserter(aa), sqabs_t<Kat>());

// インデックスを入れるベクトルを用意する
Iat ia;　std::transform(aa.begin(), aa.end(), back_inserter(ia), counter_t<Kt, It>());

// そしてソートする。比較は aa に対して行われ、ソートは ia に対して行う
std::sort(ia.begin(), ia.end(), comparator_deindexer_t<Kat::const_iterator, std::less<Kt> >(aa.begin()));

//------

// ソートされてるかチェック
Iat::iterator p = std::adjacent_find(ia.begin(), ia.end(), comparator_deindexer_t<Kat::const_iterator, std::greater<Kt> >(aa.begin()));
std::cout << ((p == ia.end())? "good job!" : "fiasco!") << std::endl;
// ソート順にもとのベクトルを出力。ia を順に参照し、kaa を出力する
std::for_each(ia.begin(), ia.end(), unary_function_deindexer_t<Kaat::const_iterator, void, writer_t<Kat> >(kaa.begin()));

good job!
( -0.188818 -0.44084 0.137486 )
( 0.364483 0.511704 0.443831 )
( -0.0494095 -0.75396 -0.264382 )
( -0.688894 0.00784326 0.464034 )
( -0.644215 0.634388 -0.0494705 )
( 0.643361 0.164098 -0.617298 )
( 0.810236 0.385784 -0.393902 )
( 0.366375 -0.693533 0.754509 )
( -0.146886 -0.859249 0.933226 )
( -0.705008 0.899167 -0.716849 )

ふふふ、二度と読みたくないコードがまた完成した。 Bjarne 的なのか、Stepanov 的なのか、単にわたし的なのか。

とうふの角

25 度だろうが 7 度だろうが春、つぼみつけすぎのクレマチス。

* * *

コーナー・キューブ、つまり 3 次元空間で x ≥ 0, y ≥ 0, z ≥ 0 みたいな無限に巨大なとうふの 1 つの角を想像する。 この角のあたりを斜めに包丁でスパッと切ると、切り方によっていろんな三角錐ができあがる。 その切片はいろんな形の、すべての、ただし鋭角な三角形。 鈍角はどこにいったのだろう。 切り口が鈍角になるには直方体じゃなく平たくつぶれたとうふじゃないとだめそうだ。 そんなものもはやとうふではない。

飽くまで直方体の無限に大きなとうふがプリズムみたいに透明だとして、切片と真っ直ぐ垂直に向き合うなら、向こう側の 3 つの辺と角が透けて見えるはずだ。 別に切片を下にしてまな板を真上から覗き込んでもいいのだけれど。 そうして見たときの、この角の位置は平面三角形でいうところの「垂心」になっている。 つまり角から切片に垂直に下ろした足もやっぱり垂心なのだ。 透けて見える辺は三角形の頂点から下ろした垂線のはずだ。 なかなか面白いと思ったが、とうふが直方体であることを考えると別にそんなに不思議じゃない。 ちなみに、三角形の「重」心は向こう側の 3 つの辺を共有する直方体の対角線と三角形が交わる点。 これも不思議じゃない。

今度は切片に垂直ではなくとうふの直方体の角の方から [(x, x, x) から] 切片の三角形の射影を眺めると、とうふの角は「フェルマー点」だ。 外心やオイラー線はわかるようでわからない。

さてこうなると鈍角三角形も見つけたい。 鈍角三角形だと垂心が三角形の外にある。 とうふの四面体をどんな風にみたらとうふの角が外にある三角形がありうるだろうかと考えてたら、あったよ鈍角三角形。 透けて見える面に隠れていた。 かくしてみそ汁には三角のとうふが浮くのであった。

意味

情報論と呼ばれるものは、情報を扱いはしない。 ある仮定のもとで情報の量について云々はするが、情報そのものをうまく捉えてはいない。 すべて、表の出る確率がこれこれで裏の確率がこれこれといった確率分布を与えた後で始まる話であり、その表裏がどのような情報であるかについてその先は問えない。 これは公理化された確率論がそもそも確率そのものを扱わず、さまざまな事象に対する確率を与えた後で、その計算方法について示したものであることを引き継いでいる。 このことは、形式論理学が世界との間で論理が意味するものを捨てて、純粋に形式の内に留まることによって成功したのと似ている。 形式と世界とのインターフェースを直視し踏み込もうとすれば、たちまちからみつく茂みに足を取られ居場所を見失ないかねない。でもぼくらが現実にすでにいばらの中にいるかもしれないのに見ないふりをするとすれば、それもあまり居心地のいい話ではない。

情報量と情報との関係も微妙だし、情報の意味が受け手にとって変わってくることもほとんど自明だ。 アラビア文字やモンゴル文字を美しいと思いこそはすれ、ぼくにはほとんどそれ以上にはなりえない。 囲碁のルールは知っていてもぼくには盤面を見てもどちらが優勢かさえわからぬただの白黒の模様だ。 自分自身の X 線写真もぼくにはそれと大差ない。 肺の影とやらがあるかどうは専門の医者に見てもらうしかない。 こうした例は枚挙に暇がないほど挙げることができる。 “Gen.11” はわずか 6 バイトの文字列に過ぎないが、聖書が手元にあれば、創世記 11 章「バベルの塔」の物語を意味しうる。 0, 1 という 1 ビットの区別が何を意味するかは文脈の数、あらゆる yes-no 疑問文の数だけ異なりうる。 ということは結局状況を好きに設定することを認めてしまえば 1 ビットであらゆる情報を意味しうる。 情報は、送り手と受け手が共通に持つもの、言語の知識や暗号の鍵や聖書という本に依存している。 であれば文脈、送り手と受け手とが共通に持つものに相対的に、あるいはそれも含めて情報を定めればよいのだろうか。 しかし共通に持つものをまともに定められそうなのは、はじめからそれを意図したネットワークや通信の規格のようなものだけだろう。 道具が臨機応変に意味するところを変え、捉えがたいのに似て、共通に持つものがどこまで共通なのかは心許ない。

英語で出てくるアルファベットを頻度順に並べると ETAOIN SHRDLU で始まり XZ で終わるとされる。 かつての鋳植機のキーボードの配列。 英語の文章を符号化するとき、アルファベットを 1 バイトずつで表すのではなく、頻度の多い E に頻度の対数に応じた短いビット列を割り当て、Z に長いビット列を割り当てるといった具合にすれば、英語でありさえすればほとんどの場合符号は元のものより短くなる。 イカサマコインが 1 ビット以下であるように、英語の文字ごとの頻度が均一でなく冗長であるからエントロピーはいくらか小さくなるのだ。 しかしこれは最良とは程遠い。 Q の後はほぼ必ず U であったり、S の後はほぼ必ず R でなかったりすることに注目すれば、2 文字目のエントロピーはさらに小さくなる。 3 文字、4 文字と増やしていけばどんどん小さくなっていく。 “When we have shuffled off this mortal ... ,” 英語文化圏の人なら『ハムレット』を読んだことがなくてもこの文に続く次の単語が coil であることはほぼ想像できてしまうのだろう。 ならば「英語文化」に相対的なこの coil の情報量は 1 ビットに満たないはずだ。 この表現自体シェイクスピアが作り出したものだとすると、少なくともその当初はそうではなかったのだろう。 しかしよほど鈍くない限り “mortal coil” という語が辞書に載る前から、それらの単語の微妙なニュアンスを読み取って、その比喩の意味するところは英語文化圏に居さえすれば自然に理解できたはずだ。 一方で、英語を他の文化圏として後から学ばねばならない人間にとっては、「死すべき者たちのコイル」が「人生のしがらみ」といった意味であるとはかなりの情報量がある。

140 バイトで表されるビット列は 2¹¹²⁰ 個、すなわちおよそ 10³³⁷ 個ある。 宇宙の水素原子の数が 10⁸⁰ とすれば、宇宙 10²⁵⁷ 個分ほど。 これを標準的な 2 進数値とみればその中には「7 の 5 の 3 乗乗」や「5 の階乗の階乗」も含まれ、ASCII 文字列と見れば、「“AB” の 70 回の繰り返し」も含まれる。 しかしこうした短い記述が与えられるものはごくごくごく一部に過ぎない。 単純な算術を駆使すれば、半分の 70 バイトまでのビット列は 2⁵⁶¹ ほどしかないのだから、半分以下に圧縮できるものは高々 2⁵⁵⁹ 分の 1, つまり 10¹⁶⁸ 分の 1 程しかない。 わずか 140 文字のビット列のほとんどは圧縮できず、ぼくらはそのほとんどを眼にすることさえない。 一方で全世界での Twitter のつぶやきは 2010 年 3 月現在 100 億、10¹⁰ ほど、ハードディスク一台に収まる。 あらゆる多様な人々のうずまく多様なコイル、加算的に積み上げられたつぶやきですら、この指数的な数の可能性の前ではほとんど無に等しい。 文字通りあらゆる本を納めたボルヘスの『バベルの図書館』に迷い込み一生さまよっても、一行でも意味のある文章に出会うことは絶望的に小さな可能性しか持ち得ない。 広大な空間から消え去りそうなほど小さな「意味」のある文章をより分けているのは何か。 あらゆる可能性からこの《世界》をより分けているのは。

確率論を世界から切り離すことで公理化したコルモゴロフは、またアルゴリズムによって文字列や数値の持つ文脈に寄らない客観的な本当の複雑さを定めようとした。 文字列や数の複雑さはそれを生成できる形式的な記述、すなわちプログラムの最小の長さとして定められる。 究極の圧縮。 どういうプログラム言語、どういう処理系かという文脈はあるが、それは定数分の違いに抑えられる。 しかしその複雑さを求めることはコンピュータにとっては計算不可能な問題であった。 究極の圧縮プログラムは存在してはならない。 そのようなプログラムを認めてしまうと、ある複雑さ以上でそれ自体が最小の記述を与えることになり矛盾する。 ベリーのパラドクス。 圧縮したい文字列より短いすべてのプログラムの生成結果を順に確かめ、文字列と比較して最小の記述を見つけ出そうとしても、それが停止するとは限らない。 停止問題。

完全なランダムノイズは、記述できるような何らの特徴を持たず、それを送ろうとすれば圧縮できず、最大の情報量を持つ。 しかし何も意味しない。 限界まで圧縮された信号はランダムノイズと区別できず、復元プログラムという鍵がないと決して解読はできない。 ある文脈、ある解読プログラムがそれの意味する長い物語を示すかもしれないが、それは文脈次第であらゆるもの、あらゆる可能性でありうる。 ならば何者でもなく何も意味しない。 文脈なしにはランダムさは何の情報も含まないのでなければならない。 しかし完全にそうだろうか。 一昔前のアナログテレビの「砂嵐」の画面はテレビの中の抵抗器の熱雑音によるほとんど完全なランダムパターンだ。 熱という完全な無知であり続ける領域から来た、圧縮できないと同時に何の情報も含んでいないパターン。 しかし、見ているとぼくらはそこにもうごめく線状のパターンを感じる。 何も情報が読み取れないはずのところにさえ、ぼくらの脳の視覚野はパターンを見つけ出そうともがき身もだえている。 この煩悶の中からこそ意味は始まるのではないだろうか。

「意味」と呼ばれるその共通のものが容易に取り出せるぐらいだったなら、形式的意味処理によって知性を模倣できるとした人工知能を作り出すことも何ということもなかったはずだ。 コンピュータがこの世に誕生した瞬間からあったその目論見は正に失敗の歴史でしかなかった。 1960 年代、ウィノグラードのプログラム SHRDLU は積み木の世界であるからこそ成功したかに見えた。 閉じられた箱庭の限定された意味の世界。 何色の積み木が他のどの積み木の上か下か、必要となる意味はそのようなものでしかない。 開かれた世界の意味をこれとして取り出すことはそれと比べるとずっと困難な話だ。 ランダムな可能性の中から意味あるものをうまくより分けなければ計算量は指数的に増大する。 フレーム問題。 ならば、ぼくらは何をやっているのか。 どうやってより分けているのか、本当により分けているのか。 しかし、ぼくが情報の意味の理解を間違っていないと自信を持つとしたら、むしろそれこそ間違っている。 理解に誤解はつきものだし、そうであるようなものでなければならない。

だが理解を相対化して意味などないというのとも違う。 意味がないと思っては、ぼくらの口はただの一言の言葉も発することはない。 昔タモリがやっていたハナモゲラ語ですら意味の境界で戯れるからこそ面白く感じる。 世界が「砂嵐」で、ものがぼくらにとって何がしかの意味を持つものとして現れてこなければ、ぼくらの眼はほとんど何も眼にすることはない。 それと定めることができなくても意味があるかのようにしかぼくらは振る舞えない。 意味があるかのように苦悶しつつ振る舞うこと、その結果として意味の世界が半ば結晶のようにしっかりと、半ばアメーバのように捉えどころなく析出してくる。

悪魔

外から見るときと内側から見るときとで状況が異なり、見るものの存在を考えざるをえないという状況のある部分は、量子論と関係なく、知識の有無と記述、すなわち情報とだけに関係したより一般的な事態なのかもしれない。 複素ベクトル空間やユニタリ変換はこの点では量子論という不思議な理論とだけ関連したガジェットに過ぎないのかも。

戦前、ハンガリーはすぐれた物理学者を数多く輩出したが、その中でもレオ・シラードは興味をそそらずにいられない人物だ。 シラードは、ナチスを逃れて亡命した後、ロンドンで連鎖反応のアイデアを思いつき、ニューヨークでアインシュタインを介して大統領にナチスの原爆開発の脅威を訴えた書簡を送り、シカゴで世界初の原子炉をフェルミとともに完成させた。 物理学が政治へと飲み込まれていく時代の中心に身をおいて、奇妙な運命から、自ら考案した原爆をいかに使わずに済むかと闘い続けた。 しかしナチス登場直前の 1920 年代、若かりしころのシラードが研究をスタートさせたころのベルリンは、敗戦の混乱とハイパーインフレに襲われてはいたものの、それでも物理学の中心地としての面目はまだ保ち続けていたようだ。 シラードはこの場所で、ある奇妙なエンジンについて思いを巡らせていた。 そのエンジンは非実用的な思考実験ではあるが、多くの物理学者を現在に至るまで真剣に検討せざるをえなくさせるものだった。 単純極まりないそのエンジンは、驚くべきことに熱から無限のエネルギーを取り出すかに見えるからだ。

シラードのエンジン^[1]

一定の温度 T の環境に置かれたこのエンジンの密閉されたシリンダはほとんど真空で分子 1 つだけが入れられている。 分子の速度は温度 T の周囲の分子の速度に従ったある分布の値をとる。 エンジンには小さな想像上の観測者がいる。 マクスウェルの悪魔の子分格なのでやはり「悪魔」とよばれるが、1 ビット程度のメモリしか必要としない。 はじめ悪魔のメモリは適当な定まった状態 s に置かれている。 エネルギーを生み出すサイクルは次のようである。 まずシリンダの中央に仕切りが入れられる。 このことによって仕切りで左右に分けられたシリンダどちらか一方にだけ分子 1 つがあることになる。 悪魔はシリンダの中を観察して、左か右どちらに分子があるかを記憶する。 例えば左なら L, 右なら R. つまり分子の位置と悪魔のメモリには相関ができ上がる。 左に分子を見出した悪魔は右半分にスライド可能なピストンを仕切りのところまで入れる。 右に分子があればその逆。 このピストンを入れる向きを区別するために悪魔の観測はどうしても必要になる。 その後、中央の仕切りを取り除く。 すると分子はピストンに衝突するたびにそれをちょっとだけ動かす。 跳ね返った分子はピストンを押して運動量を与えた分、速度が遅くなるが、容器の壁は温度 T のままなので、壁に衝突するうちにやがて元の元気を取り戻す。 つまり周囲の熱浴から熱 Q を受け取る。 そして再びピストンを押しにいく。 ピストンが容器の端までいって分子が動き回る体積が元の大きさにまでなったとき、この過程は終わる。 悪魔にとってピストンははっきり方向付けられた方向へと動き、それを使って仕事 W ができる。 つまり熱 Q が仕事 W に変わる。

分子が熱のエネルギーを回復する過程を繰り返せるだけ十分ゆっくりとピストンが動くなら、つまり物理学者がいうところの準静的に動くなら、定量的にはその大きさは Q = W = kT log_e2 となる。 k はボルツマン定数というある値で、日常の単位では 1.38×10⁻²³ ジュール/ケルビンというとても小さな値。 しかしエンジンをアボガドロ数個 (6.0×10²³ 個) も調達しとけば、絶対温度 300 ケルビン（摂氏 27℃ ぐらい）の熱浴から 1 回の動作あたり 1.7 キロジュール（0.4 キロカロリー）のエネルギーを取り出せる。 これは 100 kg のものを時速 2 km まで加速する。 なじみの程よい値なのには何か意味があるのだろう。 こうしていわゆる第二種永久機関が完成する。 つまり、こんなものは完成してはいけない。 この世界ではそんなことが起きないということは熱力学の第二法則の名で表現されているものであり、考え違いがどこかに隠れているはずだ。 こうした永久機関を標榜するかのごときものが現れれば、科学者はそのどこが問題なのか探り当てずにはいられない。

よく見ると上のエンジンのサイクルは完結していないことがわかる。 1980 年代、それまでの定説を覆し、ここに問題を見出したのはベネットという IBM の研究者だった。 このエンジンは、場所や方向がよくわからなかった熱運動からわずかながらその情報を引き出し、左右方向の運動を引き出す。 引き出された情報は悪魔のメモリに残ったままだ。 アボガドロ数の悪魔は全部でアボガドロ数ビットの情報を溜め込んでいる。 気体の動きとからまりあって相関していたこの情報は、次のサイクルのためにリセットされなければならない。 左と右、L と R として 2 つに分裂していた可能性はただひとつの状態 s にまとめられなければならない。 非可逆な操作。 ランダウアーの仕事を参照して、このとき最低でも同じだけの仕事を熱に変えることが必要なのだとベネットはいう。 分子の運動の基礎にある法則は可逆、つまり時間に前後がない。 だから見かけ上非可逆な操作は違いを見えないところに捨てているに違いない。 見るものがいないところ、つまり周囲の熱になっているのだと。

これを逆に言うなら、アボガドロ数ビットの元々リセットされているメモリが地下鉱脈あたりで発見されたら、300 ケルビンから 1.7 キロジュールのエネルギーを生み出せるはずだ。 他のエネルギー資源もそういう理解はできないのだろうか。 分子が石油や天然ガスのように炭化水素であることは二酸化炭素と水であることよりも化学物質としてリセットされたメモリに近い物質で、それがもつ秩序を利用してぼくらはテレビをみたり、冷蔵庫を動かしたり、洗濯機を回す。 最終的にそれらはすべてちょうどそのワット数だけの割合で熱エネルギーとなって室内に放出される。 日常の言葉づかいでエネルギーを消費するというとき、利用可能な自由エネルギーを意味するけれど、それは状態がわかっている一種の記憶だということになるのかもしれない。

熱に関する平衡状態の気体の振る舞いを記述する変数をいじり回しているうちに有用性が明らかになったエントロピーという概念は、平衡状態の分子運動を統計的に扱うときに再定義され、確率論の上で構築された情報量として再々定義された。 その二番目、統計力学のエントロピー S は、分子の取りうる同一視されるパターンの数 W の対数に比例する量として定められる。 自ら命を絶ったボルツマンの墓碑銘、S = k log_eW. しかし誰が何を同一視しているのだろう。 ここにも見るもののいない触れることのできないミクロと観察されアクセスされるマクロの問題がある。 マクロなものは熱力学でさんざん扱われてきたためにいかにも客観的に見える。 しかし悪魔は潜んでいないのだろうか。 それらが扱えるのは十分ほったらかしにしておいた熱平衡状態だけである。 背後の力学があらわになる小さな領域、短い時間では十分理解していたつもりのマクロな概念さえゆらぐ。 はたして悪魔からは、これらの学問はどんな風に見えているのだろう。

情報理論のエントロピーは、何か確率的にしかわからないある未知のものを知るために平均として必要となる量、確率分布がもつ不確定さのようなものを意味している。 コイン投げのように 2 つの選択肢が 0 か 1 かまったくわからず 50% ずつのときには 1 ビット。 イカサマコインであることを知っていればもっと小さい。 シラードの悪魔はシリンダを観察するとき 1 ビットの情報を得る。 かつてはこのときエントロピーが上昇するのだとの説があった。 悪魔の身になれば、ピストンの片側に分子があることを知ると、分子の取りうるパターン数 W は半減する。 系の内部のエントロピーは減少したかに見える。 観測によって悪魔にとってのエントロピーと外から見たエントロピーが齟齬をきたす。 エントロピーとは観測者に相対的な概念だ。 確率分布を所与の仮定として外からもってくる必要のある確率論にもとづいた情報理論では当たり前の話かもしれない。 散らしたぼくの机もぼくにとっては決してエントロピーは高くないのだから。

何よりも客観性に心を砕いてきた物理においても、系の中と外に観測するものの存在が紛れ込むかのようだ。 だがそう見えたものは、あまりに小さくて素朴な 1 ビットあるいは 1 キュービットの操作でしかない。 これらの観測者はなるほどそのような見方もできるかもしれないという程度のものだ。 新しいものが何かであると考えるような見方にこうした観測者は何かをもたらすのだろうか。 本当に世界を見るもの、係わるものとしての資格を持つのだろうか。 人や動物だけでなくあらゆるものが生々しい観測者だと考えてもいいのだとしたら、アニミズムかオカルティズムめいているだろうか。 逆に違いがあるとしたらそれは何なのだろう。

[1] Wikimedia Commons の画像 Szilard's_engine.svg (Htkym 作成) を改変。 licensed under CC-BY-SA 3.0 Unported.

独我論

2 キュービットの系の状態 |x〉は、2 ビットの 4 つの古典的状態 00, 01, 10, 11 に対応する 4 つの基底ベクトル |00〉 = (1 0 0 0)^T, |01〉 = (0 1 0 0)^T, |10〉 = (0 0 1 0)^T, |11〉 = (0 0 0 1)^T を使って、

|x〉 = α|00〉 + β|01〉 + γ|10〉 + δ|11〉 (|α|² + |β|² + |γ|² + |δ|² = 1)

と表される。 要するに 4 次元のベクトル (α β γ δ)^T. この α, β, γ, δ は複素数なのだけど、実数でイメージをふくらませるなら、4 次元における方向のようなもの。 ただ +|x〉と −|x〉とは実質同じ状態なので、その半分、4 次元人の見上げる空。

こうすると 2 キュービットの力学、時間に関する状態の移り変わりは 4×4 のユニタリ行列 U になる。 ユニタリは随伴行列（共役の転置行列）が逆行列に等しい U^* = U⁻¹, U^*U = UU^* = I といってもよくわからないけど、2 つのベクトル (α β γ δ)^T と (α' β' γ' δ')^T の内積 αα'^* + ββ'^* + γγ'^* + δδ'^* を保つもの、といってもやっぱりよくわからないけど、実数なら直交行列、3 次元でざっくり言えば 2 軸でまわせる地球儀をあちこちまわしてみるような、角度や大きさを変えずに向きだけ変えるような変換。 あと鏡に映して裏返すのもあり。

この 2 キュービットの各々が見るものと見られるものだとしてみよう。 前のキュービットを観測される側 A だとし、後ろを観測する側 B とする。 問題はどんな状態遷移、どんな U が観測なのかということだ。 何をしたら観測とよべるだろう。 何かを知ることだから A の状態の何かを B にコピーしたい。 でも実は A の状態を完全に B にコピーはできない。 地球儀をぐるぐる回しただけで日本列島が 2 つに増えたりしない。 ユニタリ行列ごときではそんな変換は許されようがないのだ。 クローニング不能定理。

では、A が古典的状態 0 と 1 にあるときだけうまくコピーできればよしとしてみよう。 観察者 B の初期値を決めないと U は決められないので B の方は古典的状態 0 としよう。 つまりこのとき、|00〉ならそのまま U |00〉= |00〉で、|10〉なら U |10〉= |11〉になるって条件だけでいい。 これは何のことはない。 U を例えば、

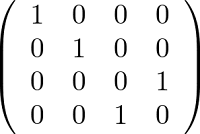
なる行列とすればいい。 これは見ての通り 3 番目と 4 番目の要素を入れ替えるだけの操作、言い換えるなら 3 番目の軸と 4 番目の軸の間に鏡を立てたような操作。 なるほどユニタリ行列になっている。

ちなみにこの U の場合、B が元々 1 だとすると、U |01〉= |01〉, U |11〉= |10〉で、A の反対になるようになっている。 実はこの行列は量子計算で制御 NOT と呼ばれている。 そこでは古典的な NAND ゲートに相当するような重要な操作。 A の側から見れば、A が 0 のとき B は状態を変えず、A が 1 のとき B はブール代数の NOT になる。 つまり、制御線 A をもつような NOT であることから制御 NOT と名付けられた。 どうも今ひとつ好きになれない名前だけど。 ここでは見られるもの A が制御するもので、見るもの B が制御されるものとなる。

この系で観測者の B は何を見るのだろう。 シュレーディンガーの猫の話では A が箱の中のアイソトープの崩壊の状態、B が箱に入れられた猫だった。 B が青酸ガスで死んじゃうのはかわいそうなので、ここではただ A を観察するだけの観察者とする。 初め、A が 0 とも 1 とも限らない一般の状態 (α β)^T にあるとしよう。 B は 0 が初期状態だから、このとき 4 次元のベクトルは α|00〉+ β|10〉 = (α 0 β 0)^T, すると上の制御 NOT を施せば (α 0 0 β)^T つまりは α|00〉+ β|11〉, エンタングルド状態。 当たり前のようで不思議なことに、通りかかった「ウィグナーの友人」C さんが蓋を開けて B に話を聞けば、0 である B は 0 である A しか見ておらず、1 である B は 1 である A しか見ていない。 蓋を開けて話を聞いた C さんにも大きな箱の系に入っていたとしよう。 このとき 3 キュービットで、α|000〉+ β|111〉. 当たり前のようで不思議なようで当たり前のことに 0 である C さんは 0 である B しか、1 である C さんは 1 である B しか知らない。

観測するということは、外から見るとこんな風にエンタングルメント、もつれあった相関を持つことらしい。 もし箱を宇宙全体に拡大してよければ、不可思議な収縮過程は必要なくなる。 宇宙とは無限次元の風見鶏の単位長さの状態ベクトル 1 つであり、すべてはどうエンタングルしてるかの重ね合わせとなる。 誰も矛盾は感じない。 大学院生エヴェレットはそう考えた。 とすると宇宙の状態ベクトルは、いろいろなエンタングルをしている観測者の重ね合わせからなっている。 そこには猫が死んだ世界とエンタングルした自分、生きている世界とエンタングルした自分がいる。 なるほど数式は単純になり、時計仕掛けの決定論の美しい神の秩序がふたたび復活する。

しかしでは、と、ふたたび疑問が持ち上がる。 独我論的疑問。 しかしでは、この私はなぜこの《私》なのか。 「この私がなぜこの私なのか」と思う重ねあわせにある多数のあなたがいるだけだよとエヴェレット派のハイパー実在論者は言うだろう。 でも、「この私がなぜこの私なのか」と思う重ねあわせにある多数のぼくの中でこの私はなぜこの《私》なのか。 問いは治まることはない。 意味のない問いだとしたら、なぜ問えると思うのか。 ここでしめされた世界の神はすべての可能性を知っているが故に何も知らないに等しい。 その世界にこの《私》がいるからこそ、この世界に新しいものを見たり、インターフェースのこちら側にいて関わりあったりするのではないか。 それは一体どういう事態なのか。 多数の私の内でこの《私》が客観的にピックアップできる存在でないとしたら、ぼくをいまここに捕えているものは何なのか。 私を《私》ということは、イヌをネコと呼んでみているだけなのだろうか。

即席量子論

1 ビットのメモリは 0 か 1 の状態しかとれない。 中間のないスイッチかシーソーのように瞬時にバタバタと値を切り替えるだけだ。 これは一番基本的で単純な状態。 ある時刻から別の時刻のメモリの状態を対応付ける関係を力学と呼んでおく。 時計仕掛けの決定論的な系というのはこれが定まるようなもの。 よそからの影響がなければある時刻の状態 x に関して別の時刻の状態 x' は、x'=f(x) のように関数で書けるだろう。 これは運動方程式を解くのに対応する。 これで 1 ビットの力学の完成。 ここには、それを見るもののいない、インターフェースのない世界。 だが状態の空間を適当に広げれば、百年後の惑星の運動を知るといったような問題でも同じ枠組みできっちり予言できる。

量子論の世界では系を見ることが状態を変えてしまうとされる。 1 ビットの量子版、1 キュービット (qubit) の状態の入れ物は 1 ビットよりぐんと大きい。 数学的おもちゃを使えば、2 次元の大きさ 1 の複素ベクトルとして書ける。 この分野では習慣的に縦ベクトルを |・〉 のような形で囲んで表すことになってる。 それぞれがビットの 0, 1 に対応する基底を |0〉= (1 0)^T, |1〉= (0 1)^T（本当は縦ベクトルのものを横に書いたので、T はそのしるし）として、1 キュービットの状態 |x〉とは、|x〉= α|0〉+β|1〉と書ける。 つまりは |x〉= (α β)^T. ここで α, β が複素数。 ベクトルの大きさは 1, つまり αα^* + ββ^* = |α|² + |β|² = 1 のもの（* は複素共役、つまり虚数部だけ −1 掛けて反転したもの）という具合になる。 だけど複素数であることはいまは本質的でないので無視すれば、これは 2 次元平面の方角、風見鶏の向きのようなもの。 ただこの風見鶏に頭と尾の区別はない。 例えば東と西が状態 0 に対応して、北と南が 1 に対応する。 しかし 0 でも 1 でもない北東とか、北北東など無数に状態が増えている。

そこにはたらく力学は風見鶏のベクトルの方角をくるくるとかえるものになる。 風見鶏の方角を変える規則はやはり関数で書ける。 しかもこういう風に書いた状態では、時刻間の状態を対応づける関数はすごく制限があって、ベクトルの大きさを変えず、他のベクトルとの間の角度を変えないような変化しかできない。 再び数学的ジャーゴンで正確にいうと、ある時刻の状態 |x〉に関して別の状態 |x'〉は、何かのユニタリー行列という行列 U を掛けるだけの変化になる、|x'〉= U |x〉. 実数に限ればこれは直交行列で回転か鏡像反転かその組み合わせとなる。

状態と力学というこの理論のここまでは、決定論的な力学であることに変わりはないという意味で古典論のビットと同じ。 量子論でのおなじみの確率の話は入ってこない。 確率的な振る舞いはこの風見鶏の向きを見ようとしたときにだけ起こる。 観測するものなんかいなければこの話はこれで終わり。 奇妙なことに風見鶏の方角をぼくらは直接知ることができない。 知ることができるのは 0 か 1 の古典的なビットの状態だけ。 風見鶏が都合よくぴったり東か西を向いていたら、つまり |0〉か −|0〉（か複素数倍）だったら必ず観察結果は 0 になる。 南北なら必ず 1. 一般の |x〉= α|0〉+ β|1〉の場合に、はじめて確率的な振る舞いが現れ、あるときには 0 であるときには 1 となる。 その確率は、それぞれ |α|²= αα^* と |β|²= ββ^*. 例えば北東を向いていれば、0 となるか 1 となるかは半々の確率。 北北東なら 0 もあるけど 1 となる確率が高い。 しかも、さらに奇妙なことに観測すると風見鶏の方角そのものが、観察結果の状態に変わってしまう。 つまり観察結果と風見鶏はある種の相関をもってしまう。 観察前、北東を向いていたはずのものが観察で 1 という結果が得られたとすると、観察後は風見鶏は北向きに「収縮」することになる。 状態と力学に、この観測と収縮といういささか余計な不思議なものが加わって 1 キュービットの世界ができあがる。 不思議ではあるけど、単に簡単な線形代数の算数の世界に過ぎなくもある。

古典的 1 ビットの状態が 0 と 1 の 2 つだったので、それに対応して 1 キュービットの話はそれらを基底とした 2 次元での方角をしめす風見鶏となった。 2 ビットでは状態は 00, 01, 10, 11 の 4 つであり、2 キュービットの状態は 4 次元の大きさ 1 の複素ベクトルとなる。 つまりそれらに対応する状態を基底として、

|x〉 = α|00〉 + β|01〉 + γ|10〉 + δ|11〉 (αα^* + ββ^* + γγ^* + δδ^* = 1)

のように書ける。 3 キュービットなら同様に 8 次元。 ついでに無数の連続した状態をもつ位置や運動量なら無限次元。 いろんな位置を波のようにうごめく関数として表される。量子は波でもあり粒でもあるといわれるが、ちゃんと住み分けがある。

2 ビットのメモリが 1 ビットのメモリ 2 つに分けられるのは当たり前のように思える。 なるほど 00, 01, 10, 11, どの場合であっても前のビットと後ろのビットの状態はきっちり分けられる。 もちろん 3 ビット以上でも同様。 だが 3 キュービットは 8 次元で表される。 1 キュービットは 2 次元なので、これだけで 1 キュービットを 3 つ張り合わせた 2+2+2 = 6 次元以上の状態をもっちゃっているのがわかる。 3 キュービットの状態は 1 キュービット 3 つの状態には分割できなくても当然なのだ。 2 キュービットでも話は同じで 1 キュービットずつに分割できないような状態がある。 こういう状態は、観測するとそれぞれのビットに何らかの相関があって、エンタングル状態、もつれあった状態とよばれる。 典型的には例えば、状態 |x〉 = 2^−1/2|00〉 + 2^−1/2|11〉は、最初のビットだけ観測したとしても、それが 0 なら 2 番目のビットも必ず 0 に収縮し、1 なら 2 番目のビットも必ず 1 に収縮する。 これがアインシュタインが顔をしかめたいわゆる EPR 相関。 1 ビット目が青酸の入ったビンの状態で、2 ビット目が猫の生死の状態を表すとすれば、これはあの不憫なシュレーディンガーの猫の話でもある。

機械仕掛けの力学の世界は見るもののいない、インターフェースのない世界だった。 量子論では奇妙な形で観測するものが関わっている。 それはひとつは系の外側から収縮をともなう観測をするものとして。 収縮は理論が扱うもののうちかどうかはっきりしない。 ちょうど系のインターフェースなのだ。 しかしインターフェースがどこにあるかよくわからない。 マクロとミクロという言葉を使って区別した人もいたし、人間の意識が収縮させるのだとした人もいた。 とりあえずこれでうまく計算できるのだから気にしないという人も。 でも客観を標榜してきた物理の理論において、見るものが現れざるをえない端的な例なのだから大いに気にしたくもある。

量子論の状態と力学は古典論と同じく決定論的で、他の理論と比べても何の問題もなかった。 力学はくるくるとねじれるだけの単純な運動で、とても美しい。 しかし量子論ではそこに何か系を見るものによる観測と収縮という余計な要素を付け加えねばならなかった。 この 2 つは、それまでの物理の理論の性質に比べるとどうにも気持ち悪い。 物理の基本法則の多くは決定論的だけでなく時間に関しても対称である。 過去と未来の区別はない。 なのに観測と収縮だけは確率論的で観測前と後で状態が急変する。 時間に関しても非対称だ。 いくらか付け焼刃にみえるし、どうみてもそれまでの美しさのかけらもない。 こんなものなかったら素晴らしかったのに。 系の境界を動かせば系の中に観測者を取り込めもする。 つまりシュレーディンガーの猫があわれな観測者だ。 2 キュービットの一方を観測されているものとして、もう一方を観測するものとしたとき、観測者は何を見るのだろうか。 見ることはどういう意味で定式化されるのだろうか。

道具

掃除機はかつてほうきとちりとりだった。 似ても似つかなくても、機能的にはそうだ。 洗濯機は洗濯板だった。 扇風機はうちわだった。 ではテレビとはかつて何だったのだろう。 ラジオだろうか、新聞だろうか、映画館か。 カメラ、ケータイ、コンピュータはどうだったか。 むしろこれらは何かの代替物として成立したんじゃない。 むしろその出現によってユーザとの間に新しい関係を作り出したものなのだ。 そんなものなくても世の中まあうまく回ってたのにそれらは現れた。 だが、今日の世の中は昨日とは変わってしまっている。 今ではもうこれらがないふりをすることはできないし、場合によってはどうしても必要なものである。 道具に対する必要は先にある必要がない。 「必要は発明の母」である必要はない。 むしろ「発明が必要の母」ともなる。 そのとき新しい関係を誕生させる何かが起こる。 何かとは何か。

あるチンパンジーの群れは手にもつ石と台となる石を使って木の実を叩き潰し中身にありつく。 木の実を車に踏み潰させるカラスもいるし、ラッコは石の上で貝を割るし、ある種のサギは水面に木の葉を落として魚をねらう。 動物を観察すればするほど道具を用いる動物がみつかる。 もはや何をして道具というかがわからなくもなってくる。 ビーバーのダムは道具なのだろうか。 ヤドカリの宿はどうだろう。 ヤドカリは本能に従うだけだというなら、ココナツの殻に身を包むタコの場合はどうだろう^[1]。 ヤドカリとタコの間の区別にどこまでこだわれるだろうか。 動物の知能や行動の不思議にただ感心するのは簡単だし、逆に知性と本能の境界線によって分類できると考えるのもよくある手だ。 だが振り返ってみれば人の道具はこれらすべてに対してどうみても特殊である。 ヒトの世界は道具にあふれており、部屋の中では見回して道具でないものを見つけ出すことさえ難しい。 ボノボやチンパンジーが X 歳の子供の知能に相当するなどと動物学者にうそぶかれたところで、彼らとぼくらの世界には何かもっと本質的で決定的な違いがあると思える。 違いは頭の良さに還元できるような問題ではない。 密林のチンパンジーに突然フォン・ノイマンの知性が与えられても、明日コンピュータを発明することはない。 彼らとぼくらの違いはぼくらの周りにある多数の道具そのものにあるのだから。

痕跡が残っている限りで人類最初の道具、オルドワン石器は石の端を打ち欠いてとがらせただけのものである。 それでもここにはチンパンジーのそれとは重要な違いがある。 石器は別の石によって加工されなければならない。 道具のための道具、道具の二次使用。 いささか強引なところはあるけれど、ここには見かけ以上の差異があると見ることができる。 ホモ・ハビリスたちのオルドワン石器だけの時代は何十万年も続いたが、道具の二次使用に進めるならば三次、四次へと進むことに何の問題もないはずだからだ。 何かのための手段であった道具は、道具の道具にとって加工する対象、目的となる対象となる。 皮を剥ぐ、肉を切る、穂を摘む、動詞を担う道具は、剥ぐもの、切るもの、摘むものとして名詞となり他の動詞の目的語となりうる。 そうした変化が本当に本質的なら、それは長く続く鎖の最初の環となったかもしれない。

無限に連なることを許されたこの連鎖はとても重大な変化だ。 このときおそらく道具と、そして言葉や人間社会とは、可能性に開かれた独自の世界の中で、後世に継承すること、伝えることのできるものを手に入れた。 オルドワンはタンザニアのオルドヴァイ渓谷の名にちなむ。 クラークがモノリスを置いた土地。 モノリスからヒトが学んだのは行為を対象とすることへの気づきだったのだろう。 こうして道具の世界が作られ、人は現在の多数の道具に囲まれる暮らしへと導かれた。 道具同士は相互に依存したネットワークによって成立している。 ありふれた 1 本のネジを作るために、いくつのネジのついた道具がかかわっているのだろうと考えるなら、相互に依存しあった道具のネットワーク、長い歴史の中で選択と発展を繰り返しそれを支えてきた社会が今ここに存在することが、ヒトを他の動物とをここまでたがえているのだと思われてくる。 人において遺伝子はもはや伝達の重要な役割を担っていない。 人において伝えられるものは道具であり、言葉であり、それらを成り立たせている社会だ。

そうした道具の 1 つが失われれば影響は全体に及んでいくだろうが、それはどの程度のものだろう。 コンピュータ上のプロセスならライブラリの致命的な単一のバグが確実にプロセス全体をだめにする。 しかしネジひとつならそこまで波及することはないと思える。 単に 2 つのものを留めておくだけなら臨機応変になにか他のもので代用できるかもしれない。 ある人は言う、鉛筆がものを書くためのものだと誰が決めたというのだと。 鉛筆の発明者か、あるいは辞書の編纂者か。 しかし手の届かない背中の辺りがかゆくなったとき、都合よくまごのてなんかが手近になければ、我慢できずに迷わず長いものなら何でも手にするだろうと。 そのとき辞書の定義を気にかけることもなく、鉛筆とは背中を掻くための道具足りうると言うべきではないか。 ネジでないものがネジとなり、鉛筆が別のものともなりうる道具の世界とは何だろう。 あるものがあるものに役立つ道具だと言うのは誰なのだろう。

最古のオルドワン石器は 250 万年前には有用な道具であったのだろう。 博物館の中の現在でもそうなのだろうか。 道具の依存関係のネットワークをグラフ構造で示すことができたとしても、道具を表したものといえるのだろうか。 しかし、遺伝子の塩基配列が生物ではないように、エディタ・プログラムのリストが文章の編集をしないように、あるいは読まれない本が何の物語も語らないように、解釈するもののいないコードは意味を持ち得ない。 名詞が再び動詞となり、ユーザが道具を使うこと、ユーザとの間の関係が道具を道具たらしめる。 ならば道具であることは曖昧な問題となる。 山は道具である、エヴェレストを征服しようとする登山家にとって。 花も道具である、恋人に送られる花束の中で。 星々はまたただの道具でしかない、星を見上げて物思いにふけるなら。 それどころか、ぼくらに現れてくるものすべてが、ぼくらにとっては道具であり、世界と思っているものは解釈されたもの、ぼくらにとって道具でしかありえないものの集まりとなる。

だがはたしてそんなことを言ってもいいものだろうか。 ぼくらは世界にぼくらにとっての解釈以上の存在もまた感じていないだろうか。 登山家が「山がそこにあるから登るのだ」とうそぶくなら、山はそんな勝手な思いなど知ったことかと「ここにいるからいるのだ」とでも言うだろう。 生物学者は、受粉の仕組みを説明し花の美しさは人のためではなくむしろ昆虫たちのためにあるのだと諭すだろう。 何千兆 km 彼方の星々はぼくらの存在など鼻にもかけていないことは明らかだ。 人の思いだけがその存在などといっていいのだろうか。 ただそれはそこにあるという思いさえ一種の道具として見ていることなのだろうか。 鉛筆もテレビもただそこにあるものと思えないのだろうか。 少なくともぼくの犬がそう思っていたことは確かだ。 ただそこにあるということと道具の役割が決まっていないということとはどう関係するのだろうか。

人を動物からたがえ発展してきた道具において、あるいはおそらく言語においても、2 つの世界の狭間において成立するものらしい。 対象の独自の世界があり、解釈し利用するものの独自の世界がある。 その関係は微妙で写像のようにきっちりと対応付けはできない。 道具は臨機応変に複数の用途をひらくし、利用者の意図は様々なものを別の道具とみなすと同時にその向こうの何ものでもない存在も感じている。 その間を往復して、ときに恣意的に選択されたものが固定したり、求めていなかったものが新たな広い可能性の世界へと導く。 ものだけの世界ならば力学系でもグラフでも何か適当な道具立てで調べられるだろう。 だがそこにはそれを見て、それを使うものがいない。 それがなければ適切な理解は得られそうにないのに。

[1] B. Keim, 「軟体動物のハイレベルな知性」 Wired Vision, 2009-12-16

インターフェース

Caps lock キー、キーボードの左小指のすぐ隣のよい位置にたたずむこのキーを、その名が示す本来の目的で使うことはほとんどないのはたぶんぼくだけじゃない。 そもそも手元のマシンでは「追加の ctrl キー」に設定されちゃってるし、それでさえもはや習慣からあまり指はいかない。 昔々、うちにあったオリヴェッティの英文タイプライターでもトグル式の固いキーがあった。 似たような位置で、大文字ロックではなくシフト・ロックだったと思う。 アームを力任せに打ち付ける手動式タイプライターでは、キータッチやストロークがどうこうなどと言ってられないぐらいにキーが重くて深く、シフトし続けながら連続した大文字を打つという作業は、小指の限界性能を引き出すに近い。 そういう意味ではこのキーもそれなりに役に立つキーだった。 だが今では、そんなものなくてもよかったのに一度決まってしまうと簡単には変えられないものの好例かもしれない。

そもそも、英文で手紙を書くわけでもないのになぜうちに英文タイプがあったのかはよくわからないが、 単に父親が仕事上キーボードの qwerty 配列に慣れるためだったのかもしれない。 パーソナル・コンピュータなるものが電器屋の店頭に並ぶしばらく前だったのだ。 よく考えればこの Q,W,E,R,T,Y といったキーの配列すべてがもはや変えられない取り決めでもある。 というより、コンピュータのすべての外界との接点にはこうした取り決めがなきゃならない。 文字を、画像を、音声を、あつかうべきあらゆるデータをさまざまな様式で符号化し、符号化は規格、何か共通の解釈手段の取り決めを必要とする。 規格は共通のものとして収斂しようとする傾向がある一方で、キー配列、文字集合、文字コード、コンテナ、コーデック、規格が規格を生み出し、概念を生み出し、現実の世界ではいささか過剰ぎみの放散もしめす。 生物の進化のプロセスと比べてみるのはそんなに変な考えじゃないだろう。 だけど進化とのアナロジーが実際どんな意味をもちうるだろうか。

新しく生まれるようなものをどうやって表したらよいかという問題だった。 だだっ広い高次元の空間を用意して、分裂していく新しい種の可能性を全部押し込め、適当な仮想的ダイナミクスの振る舞いを解析するという方法があった。 それと対になるようなものではないが、一方では事後的な進化の道筋は系統樹で表される。 遺伝的関係を追いかけるのならその過去から未来への木のような枝分かれの形、木構造が意味を持つ。 木構造。 近縁の種のハイブリッドが完全なこの木構造を壊すということはあるとしても、この図の分かれた枝が再び交わるということは基本的はまれだろう。 原核生物から真核生物への進化で起こったと思われるいくつかの細胞内小器官の共生のような、遺伝子が「水平」に移動するマーギュリス的事態はそうは起こらなかったのだろう。

しばらく前にみた科学雑誌のサイトのブログで、毛虫から蝶への華麗なる変態が、カギムシというなかなかうねうねしたキショかわいい生きた化石的生物との異種交配によって進化したのだという論文について書かれていた^[1][2]。 そのニュースはその説そのものについての説明というより、そんな風変わりな説が権威ある学術誌に掲載されたというその雑誌の特殊な査読方法の問題についてむしろ取り上げたものだった。 ちなみに、そのいくらか裏口的な論文掲載に係わっていたのは共生説のリン・マーギュリスであったりする。 仮説そのものは、専門家からみれば誤りであることが明白な珍妙な説なのかもしれない。 だが、興味深かったのはその真偽によること以上の熱心さで、こうした仮説が学術誌に載ることが批判の的とされることだ。 「決まってしまうと簡単には変えられないもの」の強さを感じもする。 科学者の共同体で受け入れられるようなものという意味で「科学的」であること、辞書で定義されている風であるという意味で言葉の使い方が正しいこと、あるいはより明確に何らかの規格に沿っていることなどに特別な熱意をもってこだわる人があることと関係するのかもしれない。

こうしたハイブリッドの少なさは生物進化に固有の物かもしれない。 進化の系統樹に似たような系統図は時間的に継承、発展するものいろいろな対象に対して描かれるが、誠実に描けば多くはもはや木構造ではなく、より一般的な矢印のかたまり、グラフとなって、同時にその端点の節すら曖昧にぼやけて一定の省略や制限が必然となる。 言語の系統図を描こうとすれば、枝はクレオール言語の出現で合体するだろうし、語彙だけの借用はそれがどんなに大量でも省略されるだろう。 どこからどこまでひとつの言語なのかは多分に政治的に決めらるところがあるし、そう考えると節もどこまで節なのかどうかわからなくなる。 日本語の方言や朝鮮半島、さらにはその北、あるいは南の諸言語など、文法構造が似通った近隣の言語同士は点と点ではなく、太古にはむしろ乱流のように入り組みながらどこかでもっとなまめかしくうごめいていたのではないかと思える。 神話、伝説、昔話、おとぎ話のような口承による情報伝達で成り立ってきた文化は、さらに民族や言語の制限も軽々と飛び越える。 何らかの依存関係があったのかなかったのか、おどろくほどの遠距離に類似したモチーフをもつ話が見つかる。 石器時代まで遡るかもしれないこうした関係を適切に図示化することはほとんど不可能なことなのかもしれない。

符号化されたコンピュータ・ネットワークの世界では、こうしたぬえのような捉えにくさから記述されたグラフのほうへ世界自らすりよってくる。 ウェブページの参照関係、Twitter のフォローやリトゥイートの関係は、節も矢印も明確なグラフ構造として書けるだろう。 ある時点での静的なグラフのクラスタとか「小さな世界」とか全体的な統計的性質はすでにいろいろ研究されているはずだ。 時間に関する発展、新しいものがどう生まれるかという点ではどうなのだろう。

Caps lock キーを再び見つめてみる。 このキーが本来の大文字ロックのままであるキーボードを使うことが避けられなければ、ぼくにとってもこのキーには、それなりにささやかな存在意義がある。 間違って caps lock キーを押してしまったときにそれを取り消さねばならないからだ。 これは生命の存在意義にそっくりだ！ つまりそんなものだれも注文していないのに、それが存在することそれ自体で自ら「意義」、必要性を生み出してしまっている、あるいは、もはや取り消せない存在意義となりうる。 何かが伝えられることそれ自体で、コンピュータとユーザの関係、インターフェースにある変化が生まれ、それ自体の居場所が生まれる。 コンピュータ側が存在することになった独自の世界。 ユーザであるぼくの方が外部の世界。 でもその間に成立する「意義」って何のことだろう。 グラフの矢印のどこにそれはあるのだろうか。

[1] E. Dolgin, “PNAS will publish controversial papers, journal says,” The Great Beyond, nature.com, 2009-10-19

[2] B. Borrell, “National Academy as National Enquirer?,” News, ScientificAmerican.com, 2009-08-24

新しいもの

何かについて伝えるという行いは、その何かそのものを伝えるように見えて、まず独自の世界が作り出されて、その決まりの中で繰り広げるようなものじゃなくちゃいけない。 要するに言葉の規則や言葉の世界のようなもの。 決まりはコンピュータ・シミュレーションのように模倣された世界を作り出すけど、もっと生々しい生き物のようなもの。

散歩中の通りがかりのイヌに向かってこっそり「ネコ」とつぶやいてみる。 そして、そのつぶやきがどんな意味をもつのか考えてみる。 言葉の決まりから自由になろうとあがいてみても、ぼくのそのつぶやきは、イヌであるべきものをネコと呼んでみたという、その決まりにあらがったというぐらいの意味しか持ちようがない。 しかし、犬はイヌである必要はなかったはずだと思える。 そう呼ばれる必要はなかったはずだ。 実際ドッグ (dog) と、あるいはフント (Hund) と、シエン (chien) と、ペロ (perro) と、サバーカ (собака) と呼ぶ人もいる。 言葉の表現と意味との対応の恣意性。 しかし一旦決められたこの決まりからはどんなにあがいても逃れるのは難しい。 私的言語の不在。

恣意性の重要さを最初に説いたのは、大乗仏教の創始者たちでないとすれば、フェルディナン・ドゥ・ソシュールだ。 だが、安易に恣意性を持ち込むことは、根拠を問う科学的な志向を終わらせてしまうかもしれない。 「偶然だ」終わり。 「虹の色は何色にどう分割されてもよかった」とは、また恣意的な差異だけが意味を持つということを語るときの言語学者お気に入りの実例。 ニュートンの権威は虹が 7 色だという考えを根付かせた。 この世界随一の大科学者は、なにやらわからぬ神秘主義的根拠から『光学』の中でレ・ミ・ファ・ソ・ラ・シ・ド・レ、音階のそれぞれの間隔に色を割り当てようとし、半音のためにわざわざあいまいな「インディゴ」と「オレンジ」を用意した。 日本でもヨーロッパでもかつては 5 色ぐらいにわけていたようだ。 ミシェル・パストゥローは『青の歴史』の中で古代ギリシャと古代ローマで著述家たちが虹を何色に分けたかを列挙し、そこに青がなかったことを指摘する。 青は嫌われ者だったらしい。

古代、日本語の青には緑色も含まれたことはよく知られている。 そのどちらもが「アヲ」であった。 それだけでなく、紫も灰色も、ときには黒も、とにかく生気のない色すべてはアヲであった。 アヲバ、アヲゲ、アヲガヘル。 これは「やまと言葉」の特殊事情ではない。 漢字の「青」は青色、緑色どちらも表しうる。 ホメロスにとってはアルキノオス王の宮殿の鮮やかな青いフリースも、アガメムノンの盾の恐ろしげな装飾を施した鋼も、大挙して押し寄せるトロイの軍船の影もすべてキュアノス (κυανός) であった。 空カエルム (caelum) が（誤って？）語源だとされることもあるラテン語のカエルレウス (caeruleus) も緑や黒などさまざまな色を表した。 東アジア、東南アジア、インド、アフリカ、インディオ、多くの人々の多くの言語でも同じであった。 対してそうでない言語もある。 例えばロシア語では暗い青スィーニイ (синий) と明るい青ガルボーイ (голубой) さえきっちりと区別するらしい。

色の分類は結局は文化ごとにソシュール的な差異の体系が発展する恣意的なものなのか。 だが、ケイらは、膨大なフィールドワークから、白黒、そして赤から順次色の差異が分裂していく一定の物語があるのだと主張した^[1]。 リンゼイらはむしろ紫外線によって水晶体が濁るために、暖かい地方では実際に緑と青の区別が困難になるのだとの説明を持ち出した^[2]。 こうした説が正しいかは別として、恣意性を安易に受け入れていたらこうした議論へ至る道を見つけ出せなかったろう。

恣意性は、時計仕掛けの世界の見方、決定論的な世界の見方を揺るがせる。 前の状態から直後の状態が一意に決まるとする規則と最初の瞬間の状態、初期状態とからなるおなじみの世界の記述の仕方。 コンピュータ・シミュレーションのように 1 ステップずつなんの揺らぎもなく更新されていく形式的で計算可能で隅々まで見渡せる偽りの世界には、形の上で恣意性をもぐりこませる余地がない。 そのためにいくらかお決まりのやり方で、空間があらかじめ広かったのだとしようとする。

机の上に逆さに立てた鉛筆がある方向に倒れはじめれば、机にあたるまでのその動きは、鉛筆の角度のようなひとつの変数の時間に関する発展として書かれるだろう。 運動方程式が規則となり、垂直に近い最初の角度が初期状態となる。 理屈の上では真逆さに置いた鉛筆は倒れない。 しかしそれは不安定であり、実際にはどんなに慎重に置いてみても、ためらいもみせずにいずれかの方向に倒れていく。 倒れはじめればもうその方向を変えることはない。 方向は恣意的に選ばれ、もはや変更できない決まりとなったかに見える。 ちょうどイヌという言葉が選択されたように。 このとき、対称性を持つ方程式とそれを収める広い空間を用意して記述され、自発的対称性の破れなどいうもっともらしい名前でよばれる。 恣意的に選択されたかのような方向は微弱な初期値の揺らぎに押し込められ、時計仕掛けの世界観は命脈を保つ。 だがこれはどこまで、あるいはどういう意味で本当なのだろうか。 新しい俗語が生まれたとき、新しい生物種が生まれたとき、その空間はすでにあらかじめ用意されていて、初期値に含まれていたことなのだろうか。 そのとき何か新しいものが生まれたのではないのだろうか。

それでも、根拠がないとみなすことが新たな別の議論をひらくかもしれない。 恣意的だと思えるものはどうやって存在しうるのかと問うことが意味を持つかもしれない。 3 つの塩基が 1 つのアミノ酸を指定する遺伝コードは、人為的に作られた CPU のオペコード表を思わせる。 端的に「コード」としか呼びようのないほどのできだ。 種々の CPU に別の機械語があるように、世界にたくさんの言語があるように、それは別のコードでもよかったはずだと思わせる。 しかし地球上の生命はすべてこの共通のコード表かそのヴァリエーションを用いている。 地球外生命がいれば、別のコードどころか RNA や DNA さえ用いていないだろうが、その例をぼくらはまだ知らない。 なぜこのようなものが自然に発生しうるのか。

しかし本当に新しく生まれたものをうまく記述できるようなやり方をぼくはよく知らない。 複雑系の研究者は「創発」という言葉を口にする。 機械仕掛けのコンピュータ・シミュレーションの中にその片鱗を見つけ出そうともがいている。 しかしまがい物であり決定論的である計算結果の中に新しいものを見るのはいったい誰なのか、それはどのような存在なのか、何をして新しいと思うのか、もどかしげにただよう霞の中につつまれている。 新しさについての何か明確な基準を求めてしまえば無いものねだりになってしまうだろうか。 そもそも作り上げられた上から下への演繹的な体系の中で新しさって何かでありうるのだろうか。 そうでない体系って何だろう。

[1] P. Kay, L. Maffi, American Anthropologist 101: 743–760 (1999) DOI: 10.1525/aa.1999.101.4.743

[2] D.T. Lindsey, A.M. Brown, Psychological Science 13: 506–512 (2002)

増えるもの

「数」がいくらでもあるというのは頭の中で成り立つような信念だけど、身の回りにあるもっと生々しい数はどのくらいの速さで増えるものなのだろうか。

一つ形のいい小石を拾い上げて、何もない平原のお気に入りの場所に置いてみるとする。 こういう小石はどのくらいここにとどまり続けるのだろうか。 いつか突風でどこかに吹き飛ばされるだろうか。 洪水や、人知れず流れを変えた小川が運び去ってしまうのだろうか。 枯れた植物や降り積もるチリからなる土が覆い隠し暗闇のうちに飲み込まれてしまうのだろうか。 あるいは長年の風雨にさらされ、そのうち風化して千々に砕けてしまうのだろうか。 いずれにしてもぼくが置いたこの小石はぼくが知らない遠い時までこのままそこに居つづけるだろう。 小石は小石、かなりの間 1 つのものとしてその個体を保ち続ける。 2 つの小石ならやはりかなりの間は 2 であり続ける。 時間に対して結晶化した永遠を想像させるこうした個数は時間と無縁に見える。 dx/dt=0.

もう少し、変化するものを考えてみよう。 時間で時間を測るのはおかしい気もするけれど、おかしいとばかり言い切ってしまえない日常の生々しさがある。 一日一日、一年一年、時間にはサイクルがあり単位があり繰り返しがある。 草花は季節に合わせ育ち、花を咲かせ、実をつけ、冬に枯れたかと思うと、次の春に同じサイクルを繰り返す。 コンピュータもサイクルで動く。 サイクルの間に一つ一つ記号を書き換えテープを動かす。 サイクルは積み重なりとして一定の変化を生み出す。 人生は積み重なる。 時間を歩みとしての距離に例えるだけのたゆまぬ動き、流れを感じる。 特に波乱のない日常の中に、こうした一定に日々の生活に応じて、同じようにいろいろなものがゆっくりと増えたりゆっくりと減ったりしていく。 ビンの中のコーヒー豆は一日一日と減っていく。 対してその脇のゴミ箱のゴミは、いっぱいになるまで日々少しずつ増えていく。 過去は少しずつ遠ざかり、将来の予定は少しずつ近寄ってくる。 こうやってぼくらは周りの時間的に一定の変化に仮託しながら時の流れを感じていく。 ぼくらに一番馴染み深い変化。 毎年 1 つずつ積み重なっていく小石のように、1, 2, 3, 4 と増えていく直線的で一次で、時計仕掛けの、変化とはそれ以外にないと誤って人々に思い込ませているような変化。 1, 2, 3, 4 という数列はどの数も前の数と 1 つ違う。 積み上げられていく小石が時間を刻む。 dx/dt=1.

しかし、昨日と同じ明日はやってこない。 父親が自らの子供時代を思い出し、どう育てようと息子は別の時代を生きる。 とりわけ近代、人々が発展という罠に捕らわれてからはそうである。 変化にはぼくらが想像する以上の、日々の積み重ね以上の何か実質的な中身がある。 実質的な中身を数だけで捉えられるなどとは思えない。 しかし数はそれを反映して何かを示している。 何かを作りだすのは集団だ。

1 人の有名人が街角にたたずめば何事かと人々が集まってくるだろう。 やがて集団は幾重にも円環を描く塊となる。 円は面倒なので碁盤目のように人々が並ぶとしてみよう。 1 人の人の前後左右、その四隅に 1 列目の人が並ぶ。 ここには 3×3、9 人の人がいる。 次にその外側、2 列目までに並ぶ人々は、5×5、25 人。 人々の輪が大きくなるに従い、人々の数は 1, 9, 25, 49, 81 と増えていく。 中心の人が有名であること、集団の中で抜きん出ていることは、一人が一人ずつ接する日常とは何か違うものを作り出す原因となっている。 2 次元の平面に集まる人を表すこの数列は奇数 1, 3, 5, 7, 9 の 2 乗、2 次の変化だ。 このときその差、8, 16, 24, 32 の中に前に見た数列 1, 2, 3, 4 を見出す。 8 つずつにはなっているが、これは積み上げた結果としての直線的変化だ。 dx/dt=t.

この過程を繰り返すなら、次に 3 次の、その次に 4 次の変化を見つけ出すだろう。 積み重ね、積分は次数を 1 つ上げる。 こうして多様な変化が生まれる。 こうした変化は増えるだけではなくときに減ることもする。 2 次式、パラボラはひとつの山あるいは谷を持つ。 3 次式には山と谷の両方があるかもしれない。 10 次式は 9 つまでのこうした極値をもちうる。 時間に関する多項式的変化、あるいはそれで近似されるようなサイクル的な変化がこうして生まれる。 ぼくらは世界の変化を多項式や三角関数に当てはめようとする。 あらゆる変化を記述しようと試みる。 惑星の動きは、回転と、それを補正するたくさんの周天円、あるいは摂動項に分解される。 さらに日々の気温を景気を、世界のあらゆる変化をそうしてフィッテングしようと試みる。 世界は記述されたのだろうか。

しかし世界はそうした試みをあざ笑っている。 記述されたかのような軌道は、ほんのわずかにずれていく。 わずかに見えたそのずれは急速に拡大していく。 1 次、2 次、3 次、4 次、あらゆる多項式を上回る速さで現実の世界は逃げていく。 予測しようとした試みを許さない何か、人々がカオスとよんだ何か。 こうした変化のすさまじさをぼくらは知らなかったわけじゃない。 でも日常の変化に引きずられて、いつか必ず破綻するはずのネズミ講式の罠に引っかかる。 これは愚かで不幸な一部の人たちの話ではない。 近代に生きながら昨日と同じ明日がくると思っているすべての人が、必然のように足を踏み入れざるをえない罠だ。

こうしたある値の急速な増加は、時間の変化がその値そのものに寄るときに起こる、dx/dt=x. これは指数関数という名が与えられた多項式の無限の重なりの中に潜む x = 1 + t + t²/2 + t³/6 + t⁴/24 + ... = e^t.

ひとつのやや肥太り気味の原子に小さな中性子があたると、原子は 2 つに分かれ、光や何かの他にいくつかの中性子を出す。 こうして複数に増えた中性子が適当な速度で別の原子にあたると同じ過程が繰り返される。 ひとつの過程で中性子が 2 倍になるのなら、中性子の数は 1, 2, 4, 8 と増えていく。 10 ステップ目には 1024 であったものが、20 ステップ目には 1 048 576 に、30 ステップ目には 1 073 741 824 になる。 この急速な拡大を連鎖反応による核爆発とよぶ。 拡大を指数関数、ネズミ算、複利、いろいろ別な名前で呼んでも似たようなものだ。 中性子の数の時間の変化はその数そのものに寄っている。 しかし、それそのものに寄るものの代表格は生物だ。 栄養たっぷりのシャーレに大腸菌を 1 匹入れれば、分裂するごとに 2, 4, 8, 16, 32 と増え続ける。 シャーレの中の大腸菌はエサが足りなくなったり、シャーレにいっぱいになればもうこんな拡大は続けていられない。 ネズミ講の始まりと終わりでその状況が天と地であるのと同じように、このとき大腸菌を別の状況が支配する。 これは昨日と同じ明日にならない別の例となる。

こうした指数関数的拡大を手ごろなサイズに手なずける方法は知っている。 それが数そのものといってもいい。 さっきの 10 ステップごとの数列 1, 1 024, 1 048 576, 1 073 741 824 では桁数がおよそ 3 桁ずつ増えていく。 数は 1024 倍に増えるが、桁数は 3 つずつ、1, 4, 7, 10, 見慣れた直線的な増え方だ。 ここにちょっとしたごまかしがある。 1 073 741 824 という数を表すのに 1 073 741 824 個の点を示す代わりにぼくらは 10 個の数字を書きつらねて済ます。 しかし数字の列 1 073 741 824 はどういう意味で数 1 073 741 824 なのだろうか。

さらに指数関数を上回って増えるものもたくさんある。 組み合わせ爆発的な階乗 1, 2, 6, 24, 120. いつ終わるか期待できるような計算では計算できないアッカーマン関数、計算するプロセスそのものがないビジービーバー関数。 しかし計算論的お遊びとばかりいっていられないものもある。 人類の人口は、ギザのピラミッドが作られたころ 1 億人だった。 2 千数百年後イエスがいたころには 2 億人になった。 4 億人になるのは千数百年後の 14 世紀ごろである。 その後、ルネッサンス、産業革命で弾みがついていく。 17 世紀 8 億、19 世紀半ば 16 億、1963 年 32 億、2003 年 64 億。 倍になる間隔はだんだんと短くなる。 そろそろ地球もいっぱいになったという意味で 21 世紀前半は人類最大の転換点だけど、ここまでは大腸菌より元気にやってきた。

地球上の人間はシャーレの中の大腸菌と何が違ったのだろう。 dx/dt=x² ということはあるだろうか。 媒質の中にちょっぴり X という分子があって、たまさか別の X と出会ったときに、周りの物質を X に変えちゃうのだとしよう。 細かい定数を気にしなければ初めのころの X の増え方は dx/dt=x², よって、x=−1/t, 見慣れた双曲線、ハイパーサイクル、自己触媒。 この変化は急速に拡大するどころか有限の時間で発散してしまう。

そうだとすると自己触媒となっているものは何だろう。 ハイパーサイクルは遺伝的記号を固定化するのに役立ったという仮説として現れてきた。 恣意的でありえた記号が固定化されるプロセスには何があるのだろうか。 伝わるものの特性とは何か。