2 キュービットの系の状態 |x〉は、2 ビットの 4 つの古典的状態 00, 01, 10, 11 に対応する 4 つの基底ベクトル |00〉 = (1 0 0 0)T, |01〉 = (0 1 0 0)T, |10〉 = (0 0 1 0)T, |11〉 = (0 0 0 1)T を使って、
と表される。 要するに 4 次元のベクトル (α β γ δ)T. この α, β, γ, δ は複素数なのだけど、実数でイメージをふくらませるなら、4 次元における方向のようなもの。 ただ +|x〉と −|x〉とは実質同じ状態なので、その半分、4 次元人の見上げる空。
こうすると 2 キュービットの力学、時間に関する状態の移り変わりは 4×4 のユニタリ行列 U になる。 ユニタリは随伴行列(共役の転置行列)が逆行列に等しい U* = U−1, U*U = UU* = I といってもよくわからないけど、2 つのベクトル (α β γ δ)T と (α' β' γ' δ')T の内積 αα'* + ββ'* + γγ'* + δδ'* を保つもの、といってもやっぱりよくわからないけど、実数なら直交行列、3 次元でざっくり言えば 2 軸でまわせる地球儀をあちこちまわしてみるような、角度や大きさを変えずに向きだけ変えるような変換。 あと鏡に映して裏返すのもあり。
この 2 キュービットの各々が見るものと見られるものだとしてみよう。 前のキュービットを観測される側 A だとし、後ろを観測する側 B とする。 問題はどんな状態遷移、どんな U が観測なのかということだ。 何をしたら観測とよべるだろう。 何かを知ることだから A の状態の何かを B にコピーしたい。 でも実は A の状態を完全に B にコピーはできない。 地球儀をぐるぐる回しただけで日本列島が 2 つに増えたりしない。 ユニタリ行列ごときではそんな変換は許されようがないのだ。 クローニング不能定理。
では、A が古典的状態 0 と 1 にあるときだけうまくコピーできればよしとしてみよう。 観察者 B の初期値を決めないと U は決められないので B の方は古典的状態 0 としよう。 つまりこのとき、|00〉ならそのまま U |00〉= |00〉で、|10〉なら U |10〉= |11〉になるって条件だけでいい。 これは何のことはない。 U を例えば、
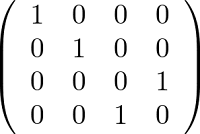
なる行列とすればいい。 これは見ての通り 3 番目と 4 番目の要素を入れ替えるだけの操作、言い換えるなら 3 番目の軸と 4 番目の軸の間に鏡を立てたような操作。 なるほどユニタリ行列になっている。
ちなみにこの U の場合、B が元々 1 だとすると、U |01〉= |01〉, U |11〉= |10〉で、A の反対になるようになっている。 実はこの行列は量子計算で制御 NOT と呼ばれている。 そこでは古典的な NAND ゲートに相当するような重要な操作。 A の側から見れば、A が 0 のとき B は状態を変えず、A が 1 のとき B はブール代数の NOT になる。 つまり、制御線 A をもつような NOT であることから制御 NOT と名付けられた。 どうも今ひとつ好きになれない名前だけど。 ここでは見られるもの A が制御するもので、見るもの B が制御されるものとなる。
この系で観測者の B は何を見るのだろう。 シュレーディンガーの猫の話では A が箱の中のアイソトープの崩壊の状態、B が箱に入れられた猫だった。 B が青酸ガスで死んじゃうのはかわいそうなので、ここではただ A を観察するだけの観察者とする。 初め、A が 0 とも 1 とも限らない一般の状態 (α β)T にあるとしよう。 B は 0 が初期状態だから、このとき 4 次元のベクトルは α|00〉+ β|10〉 = (α 0 β 0)T, すると上の制御 NOT を施せば (α 0 0 β)T つまりは α|00〉+ β|11〉, エンタングルド状態。 当たり前のようで不思議なことに、通りかかった「ウィグナーの友人」C さんが蓋を開けて B に話を聞けば、0 である B は 0 である A しか見ておらず、1 である B は 1 である A しか見ていない。 蓋を開けて話を聞いた C さんにも大きな箱の系に入っていたとしよう。 このとき 3 キュービットで、α|000〉+ β|111〉. 当たり前のようで不思議なようで当たり前のことに 0 である C さんは 0 である B しか、1 である C さんは 1 である B しか知らない。
観測するということは、外から見るとこんな風にエンタングルメント、もつれあった相関を持つことらしい。 もし箱を宇宙全体に拡大してよければ、不可思議な収縮過程は必要なくなる。 宇宙とは無限次元の風見鶏の単位長さの状態ベクトル 1 つであり、すべてはどうエンタングルしてるかの重ね合わせとなる。 誰も矛盾は感じない。 大学院生エヴェレットはそう考えた。 とすると宇宙の状態ベクトルは、いろいろなエンタングルをしている観測者の重ね合わせからなっている。 そこには猫が死んだ世界とエンタングルした自分、生きている世界とエンタングルした自分がいる。 なるほど数式は単純になり、時計仕掛けの決定論の美しい神の秩序がふたたび復活する。
しかしでは、と、ふたたび疑問が持ち上がる。 独我論的疑問。 しかしでは、この私はなぜこの《私》なのか。 「この私がなぜこの私なのか」と思う重ねあわせにある多数のあなたがいるだけだよとエヴェレット派のハイパー実在論者は言うだろう。 でも、「この私がなぜこの私なのか」と思う重ねあわせにある多数のぼくの中でこの私はなぜこの《私》なのか。 問いは治まることはない。 意味のない問いだとしたら、なぜ問えると思うのか。 ここでしめされた世界の神はすべての可能性を知っているが故に何も知らないに等しい。 その世界にこの《私》がいるからこそ、この世界に新しいものを見たり、インターフェースのこちら側にいて関わりあったりするのではないか。 それは一体どういう事態なのか。 多数の私の内でこの《私》が客観的にピックアップできる存在でないとしたら、ぼくをいまここに捕えているものは何なのか。 私を《私》ということは、イヌをネコと呼んでみているだけなのだろうか。