2020年4月26日日曜日

観測された感染者数に関する覚書き 3

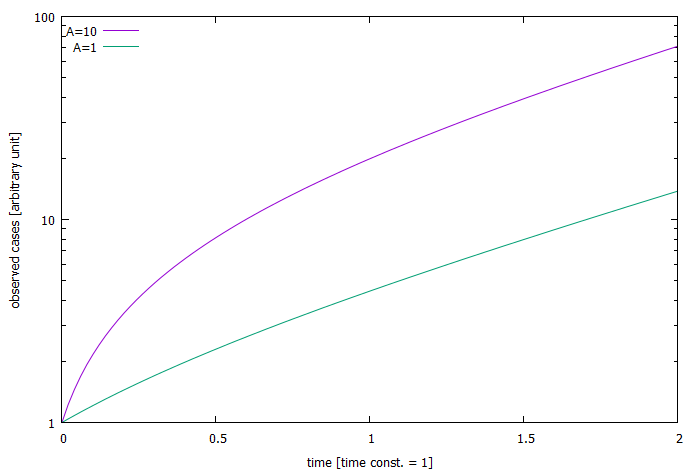
前記事で用いた $I_E(t\,;t_P)$ および $c_E(t\,;t_P)$ を、韓国・ドイツ・日本の 3 か国およびアメリカ・ニューヨーク州について示し、それぞれについて検討する。 データにはジョンズ・ホプキンズ大学 CSSE が公開している 2020 年 4 月 23 日までの時系列データを用いた（差分を取るため 4 月 22 日が $t_P$ となる）[1]。

韓国

韓国においては 2020 年 2 月 18 日に大邱（テグ）市で宗教団体に関係する感染者が見出だされ、翌 19 日に集団感染が発生していることが把握された。 その後、宗教団体に関係する者に関しては全数検査が行われた。 3 月 8 日の時点において、この集団感染による感染者が 4500 件近くあり、韓国の感染者の 6 割以上を占めていることが韓国における感染の特徴と言える[2]。 長期的に見れば、3 月後半以降、現在までに 2500 人程度の新たな感染者が見つかっており[1]、それもよく防がれているように見える。 しかし全体としてみれば発見の量は初期の動きに比べ小さい。 よって、これらはここに示した感染拡大初期に関して $I(t)$ および $c(t)$ の比較的よい近似を与えているものと思われる。

図に示されていない範囲で起こったと思われる大規模な集団感染時には、$I(t)$ の名目上の倍加時間は短かったといえるかもしれない。 しかし、それは飽くまで集団感染に起因するものである。 大邱での大規模な検査が始まった時点での観測された感染者数 $H(t)$（上図灰色の実線）の急激な上昇は多数の検査を行った帰結であり、隠れた感染者 $I(t)$ はその時点ですでに数千人いたとするのがもっともらしい。 仮にこの時期に感染自体の倍加時間 $D$ が 2-3 日のように短かい期間で拡大したのだとしても、上図のように検査と隔離の効果で増加は抑えられており、後に徐々に減少したのではないかと思われる。 実際には、初期の隠れた感染者 $I_0$ がもっと多く、$D$ がもっと長かったとして矛盾はない。 初期の韓国においては限定された集団を無症状者も含めて網羅的に検査できたことが、その後の $I(t)$ の減少に大きく寄与したと考える。 徹底した早期の検査がその後の感染拡大をうまく喰い止めた例は、規模は異なるが日本の和歌山県における病院での集団発生後の状況も事例として挙げられるだろう。

検査率を上から抑える $c_E(t\,;t_P)$ のグラフは概ね高い値を示し、倍加時間が長い場合も、初期の検査で隠れた感染者を 1 日あたり数 % のオーダーで見つけ出していたものと思われる。 $I_0$ の見積もりと合わせれば、最初の記事で述べた $A = c I_0$ はオーダーとして初期に 100 人/日程度であったろう。 例として、大邱の集団感染発覚当初からしばらくたった状況を考え、$H^* = 1000$ 人とすれば、2 月 25-26 日にこの基準を超える。 一方、2 月 23-28 日の見かけの累積確定例時定数は約 3.7 日（倍加時間約 2.6 日）の依然として短いものであった。 これより仮に $A/H^* \approx 0.1$ として、$d(\log \tilde{H})/dt = \lambda + A/H^*$ の関係を用いれば、実際の時定数は $1/\lambda \approx 6$ 日（倍加時間約 4 日）となり、検査によるの見かけの効果が実際に働いていたであろうことが裏付けられる。

ドイツ

ドイツで本格的に検査が拡大したのは 2020 年 2 月 26 日頃だが、政府が拘束力のあるロックダウンの措置を行ったのは 3 月 23 日だった[3]。 検査数は 3 月半ば頃より拡大され、1 日あたり 5 万件の大規模な検査が行われてきた[4]。 3 月下旬からは無症状者への検査も行われた[3]。 観測された感染者数（累積確定例）は、3 月中旬ごろまでおおむね倍加時間 3 日ほどであった。

極端に短くない倍加時間 ($D \geq 4$) を考えたとき、グラフから、ドイツにおいて観測された累積の感染者数 $H(t)$（灰色）が隠れた感染者数の下限 $I_E(t\,;t_P)$（実線）を超えたのは、ロックダウンが発令された 3 月下旬に入ってからであることがわかる。 すなわち、そのころには少なくともまだ把握された感染者と同等以上の隠れた感染者がいたことになる。 仮に、3 月 18 日時点で、観測された感染者の 5 倍の隠れた感染者がいたとしたとき、一定の倍加時間のもとそれ以前の感染者数がどのようであったかを破線で表している。 前出の $I_R$ に相当するこの追加の感染者は単純に指数関数的に増大するので、この程度の大きさであった場合、下限 $I_E$ との初期の比はずっと小さくなる。 よって、これらの時点で韓国ほどには初期換算感染者を削りきれていないであろうドイツにおいても、検査初期の 2 月 25 日に数千程度の隠れた感染者がいたとすれば、見かけと異なって倍加時間 4 日以上で拡大していたとして矛盾はない。

検査率の最大値 $c_E$ は、3 月初めごろまでは韓国より小さな値を示しており、長い倍加時間を想定した場合、1 日 1 % に満たないものだった。 よって、$A$ の効果もこのころには韓国より 1 桁ほど小さかったかもしれない。 その後、$c_E$ は急激に上昇しており、実際の検査率も同様の傾向があったと思われる。 このことは、ドイツの初期の倍加時間が韓国ほど短くなかったことを説明するかもしれない。

初期の倍加時間を 6 日とした場合、ロックダウン宣言の 3 月 23 日までに削った初期換算感染者数 $J(t)$（起点 2 月 26 日）は約 3100 人、倍加時間 3 日とした場合、約 490 人である（前記事の図参照）。 これは、広範な検査と隔離とが行われなかった場合、3 月 23 日までの 26 日間で、それぞれ約 6 万 2 千人と約 20 万人に拡大したはずのものとなり、判明した感染者の隔離が適切に行われているなら大規模な検査には隠れた感染者の削減に大きな効果があったことがわかる。

ニューヨーク州

大規模な感染拡大がみられたニューヨークでは、最初の確定例が見つかった 2020 年 3 月 1 日（JHU CSSE データでカウントされたのは翌 2 日）以降、検査による累積確定例の急激な上昇が見られた。 3 月 5-19 日の見かけの倍加時間は 1.8 日であった。 一方、2020 年 4 月 23 日のニューヨーク・タイムズは、3 月 1 日の時点で実際には（ニューヨーク市のみで）1 万人を超える隠れた感染者がいたのだとするノースイースタン大学の研究グループの研究を紹介している[5]。 4 月 25 日現在、研究の詳細は明らかでないが、この値は倍加時間がある程度長いとした場合の隠れた感染者の最小値 $I_E$ と矛盾しない。 図では $I_E$ が 1 万より小さい倍加時間 6 日以下の場合に関して、3 月 1 日の時点で 1 万人の隠れた感染者がいたとした場合のその後の隠れた感染者数を破線で示している。

日本

観測された感染者数 $H(t)$ や、それによる初期換算感染者数 $J(t)$ で特異的な少なさを示している日本においては、$I_E$ および $c_E$ のグラフも特異的なものとなっている。 パラメーターの倍加時間にあまり依存せず、隠れた感染者の最小値 $I_E$ は $H(t)$ に沿って増加し、検査率の最大値 $c_E$ は時間に依存しない大きな一定の値を示している。 検査の強い抑制によって、これらは実際の値と大きく離れたものでありうる。 しかし、検査の強い抑制が一定の基準で行われ続けていると考えるなら、$c(t)$ がほぼ定数となることと、$H(t)$ のほぼ一定の時定数が隠れた感染者 $I(t)$ のそれを反映していることとは想定しうるだろう。

2 月 15 日から 30 日間の倍加時間はおよそ 7 日であり、これが初期の $I(t)$ の倍加時間も反映していると思われる。 このときの $I_0$ の最小値、すなわち検査が削った初期換算感染者数は 240 人程であるが、4 月下旬も隠れた感染者が少なからず存在していることを考えれば、起点とした 2 月 14 日の感染者はこれよりはるかに多かった。 図では、$I_0$ が 1000 人とした場合と 10000 人とした場合のその後の動きを破線で示している。 隠れた感染者は検査からほとんど影響を受けることなく、ほぼ指数関数的に増大する。 倍加時間 7 日が続いていたとした場合、これらの $I_0$ による 4 月 1 日（47 日後）の隠れた感染者数は、それぞれ約 8 万 6 千人と、約 103 万人となる。

*   *   *

結局、観測された感染者数の動きを隠れた感染者数と正しく区別して論じるならば、日本の観測された感染者数の少なさを、日本の隠れた感染者数がヨーロッパ諸国で想定される値よりもずっと小さいとする根拠とすることはできないことがわかる。

「新型コロナウイルス感染症対策専門家会議」は2020 年 4 月 1 日の資料においていわゆる「オーバーシュート」に関し「我が国では、今のところ諸外国のような、オーバーシュート（爆発的患者急増）は見られていない」として、次のような注釈を加えた[6]。

オーバーシュート： 欧米で見られるように、爆発的な患者数の増加のことを指すが、2～3 日で累積患者数が倍増する程度のスピードが継続して認められるものを指す。異常なスピードでの患者数増加が見込まれるため、一定期間の不要不急の外出自粛や移動の制限（いわゆるロックダウンに類する措置）を含む速やかな対策を必要とする。（後略）
さらに太字とアンダーラインで強調し、
いわゆる「医療崩壊」は、オーバーシュートが生じてから起こるものと解される向きもある。しかし、新規感染者数が急増し、クラスター感染が頻繁に報告されている現状を考えれば、爆発的感染が起こる前に医療供給体制の限度を超える負担がかかり医療現場が機能不全に陥ることが予想される。
とした。

すなわち専門家会議によれば「オーバーシュート」は「欧米」で見られたような単に倍加時間 2-3 日の継続的拡大を意味するとし、このような短い倍加時間による増大がなくとも、医療のリソース不足による機能不全が迫っていることに警鐘を鳴らした。 しかし、この小論で明らかとしたように、ヨーロッパ諸国やアメリカの都市で初期に見られたこのような短い倍加時間の「爆発的急増」は大規模な検査を行うことによってすでにいた隠れた感染者を発掘した見かけの効果だろう。 日本が検査数を絞っているが故に、日本においてはそのような増加は見えず、逆に日本でも諸外国でもそれよりはやや長い一定の倍加時間での指数関数的拡大を継続的に続けている。 この点で日本の状況は何ら諸外国と変わる点を見出だせない。 違いは、日本の倍加時間が幸いにもヨーロッパなどよりやや長いと思われることと、逆に日本がほとんど検査を行っていないために感染者を適切に削っていくことができなかったことである。 指数関数的拡大を続ける限り、倍加時間の多少の長短にかかわりなく医療崩壊のような同等の帰結がもたらされるのは当然である。

「オーバーシュート」(overshoot) の語は、本来、なにがしかの量に対して、他の要因から想定したなにがしかの基準が先にあり、実際の量がそれを超えていくことを表すのに相応しい語である。 そうした他の要因が見えない「爆発的急増」もしくは「倍加時間 2-3 日」を単に表すとした用法は甚だ奇妙にみえる。 ここからは想像であるが、むしろその基準は上の言と逆に専門家会議こそが医療崩壊を想定していたのではないか。 倍加時間 2-3 日という事態が実在のものと思い込み、そのような事態になれば否応なくすぐさま医療崩壊に至ると考えたとするならば、「オーバーシュート」という語を用いた意味が理解できる。 実際には、そのような増加がなくとも隠れた感染者数は長めの倍加時間での指数関数的増大を続け、医療崩壊が想定される状況まで至ったために、医療崩壊と関係しない「オーバーシュート」＝「爆発的増加」という本来の語の意味と合わない置き換えが成立したのではないだろうか。 もしそうだとすれば、専門家会議は自らが立てた不適切な道標によって自ら勝手に道を誤っていることとなる。

投稿者 時刻: 0 件のコメント:

2020年4月18日土曜日

観測された感染者数に関する覚書き 2

（2020 年 4 月 25 日に改稿し、実データを用いた解析は後続の別記事としました）

再掲した下図からも明らかなように、疫病を終息させることは隠れた感染者 $I$ を消滅させることであり、そのためには $I$ を増加させる感染率 $a$ を減らすか、$I$ を減少させる検査・隔離率 $c$ を増やすかする以外にない（自然の回復率 $b$ を人為で変えることは難しいだろう）。 ロックダウンや社会的距離を保つといった政策は $a$ を減らすことに該当し、広範な検査を行うことは $c$ を増やすことに当たる。 この両面作戦のうち、日本は $c$ を増やすという手段をほとんど採ることなく、結果として $I$ の大きさも推測し難いものとなっている。


疫病の終息は、$a$ を減らし $c$ を増やすことで $a - b - c < 0$ に持ち込むことが前提となる。

感染率 $a$ と検査率 $c$ を推測する何らかの方法なしには観測された感染者数（われわれが感染者数として把握しているもの）である $H$ から、隠れた感染者数 $I$ を推測する方法はあまりない。 特に少ない $H$ しか捉えていない日本ではそうだろう。 ただしわずかながら（ある仮定のもとで）、$H$ の増分の時系列データから、検査によってどの程度の潜在的な感染を防いできたのかを推定でき、そこから $I$ を下から抑える（それよりも小さくはないと言える値を求める）ことはできると思われる。 これによって特に、検査開始時にいたであろう隠れた感染者数 ($I_0$) とそのときの検査率（$c(0)$: 単位時間あたりに隠れた感染者のうちどれだけの割合を検査で捉えたか）に対するおおよその見積もりが与えられる。

*   *   *

少なくとも感染率 $a$ を減少させるような強力な政策が行われなかった初期において、$a$ （および $b$）を一定とみなすことができるとする（$c$ は時間の関数とする）。 このとき、前の記事のように、隠れた感染者数 $I(t)$ と観測された（検査・隔離された）感染者数 $H(t)$ の時間変化は、それらが人口に比べまだ小さいとき、 $$\dot{I}(t) = (a - b - c(t)) I(t), \quad \dot{H}(t) = c(t) I(t)$$ と見ることができる（ただし、時間微分を上付きのドットで表した）。 $\dot{H}(t)$ は、われわれが（少なくとも日ごとの差分として）知ることができる値であり、$a, b$ はパラメーターとして仮定される。 これらから、 $$\dot{I}(t) = (a - b) I(t) - \dot{H}(t)$$ よって、$I(t)$ は、 $$I(t) = \left(I_0 - \int_0^t \dot{H}(u)\,e^{-(a - b) u} du\right) e^{(a - b) t}$$ となる。

上式に含まれる積分、 $$J(t) = \int_0^t \dot{H}(u)\,e^{-(a - b) u} du$$ は、検査によって隔離された感染者数を $t = 0$ 時点に換算した人数だとみることができる。 この $J(t)$ を（$t$ までに観測された感染者の）「初期換算感染者数」と呼ぶこととする。

より詳しく言えば、時刻 $t = 0$ における感染者 1 人は隔離がなされなかったとき、時刻 $t$ で $e^{(a - b) t}$ に膨らみ、逆に $t$ における感染者 $h$ 人は、$t = 0$ において $h e^{- (a - b) t}$ 人から広まったと考えられる。 $h$ が各時点での検査を経た時間あたりの隔離者 $\dot{H}(t)$ であれば、$J(t)$ は時刻 $t$ までの検査・隔離者が $t = 0$ において何人であったかに換算した人数である。

$a$ と $b$ が一定というここでの仮定のもとで、時刻 $t$ においても隠れた感染者であり続ける集団の数は、$I_0$ から $J(t)$ を除いた残りの人々が拡大したものと捉えられ、上式、 $$I(t) = (I_0 - J(t))\,e^{(a - b)t}$$ が確かめられる。 ここでのように感染者数を初期時刻 $t = 0$ に換算して眺めるなら、検査による感染者の発見と隔離とは、$I_0$ から感染者を削っていく作業だと見ることができ、上の因子 $I_0 - J(t)$ は時刻 $t$ までにそれが削られた残りの量を表している[1]。 そして他方の因子 $e^{(a - b)t}$ が示すように、その作業は時間が経つほど指数関数的に困難なものとなる。 すなわち、感染拡大防止のためには初期に広範な検査を行うことが極めて有効であることを意味する。

*   *   *

$a - b$ または倍加時間 $D = \ln 2/(a - b)$ の値を仮定すれば、日々公表されている国や地域別の観測された確定者の人数によって $J(t)$ を評価できる。 以下の表は、ジョンズ・ホプキンズ大学 CSSE の確定者時系列データに基づきドイツ、イタリア、韓国、日本の 4 か国に関してこの換算人数を求めたものである（2020 年 4 月 15 日までのデータに基づく）。 なお、$t = 0$ となる起点にはそれぞれの国で検査がある程度まとまって行われ出した日を取っている。 また、図は $t$ に関する $J(t)$ の変化を通常のグラフと片対数グラフで表す。 起点として取った時刻から時間が経過すれば、検査による $J(t)$ の上昇は相対的に小さなものとなっていく。

検査・隔離により除かれた初期換算感染者数 $J(t)$
起点D = 3 日D = 5 日D = 7 日
ドイツ2020-02-26527 人2966 人7589 人
イタリア2020-02-211007 人4128 人9551 人
韓国2020-02-201134 人2207 人3119 人
日本2020-02-1548 人111 人218 人

韓国を除く各国で 4 月 15 日現在、まだ隠れた感染者が多く残っていると思われることを考えるなら、初期の感染者 $I_0$ はこれらの数字よりも大きなものであった。 また日本においては特異的に、検査人数が隠れた感染者の削減に直接寄与していないだろうことがここからも見て取れる。 日本と他国との比は 10 倍を超えるものとなっており、初期感染者数 $I_0$ がそれぞれの国で同等であったとするなら、これは観測された感染者が隠れた感染者よりも大きく下回っているであろうことを示唆する。

*   *   *

上で検査で感染者を見つけることは、初期換算感染者に換算するとき、検査開始時に市中あった隠れた感染者 $I_0$ を削っていく作業であると捉えられることを見た。 しかし、$I_0$ そのものは不明であり、ひいては隠れた感染者 $I(t)$ がどこまで拡がっているのかも一般に直接知ることはできない。 ただし感染が終息したなら、事後的に推測できる。 仮に時刻 $t^*$ において隠れた感染者 $I(t^*)$ を 0 にできた（終息した）とする。 このとき、$J(t^*) = I_0$、すなわち検査による初期換算感染者数が $I_0$ をすべて削ったこととなり、過去の $I(t)$ の動きは、 $$I(t) = (J(t^*) - J(t))\,e^{(a - b) t}$$ として表される。

現在時刻 $t_P$ が終息以前 $t_P \leq t^*$ の場合、過去の時刻 $t$ $(0 \leq t \leq t_P)$ における隠れた感染者 $I(t)$ は部分的にのみ判明しており、それを初期換算した感染者数 $I_0 - J(t)$ は未知の部分と既知の部分に分けられる。 $I_0 - J(t_P)$（上図ピンク色部分）は、現在時刻 $t_P$ における隠れた感染者 $I(t_P)$ に相当する部分であり、依然その大きさを定められないが、$I_0 - J(t_P)$ は $t$ によらず、自然な感染拡大の時定数 $1/(a - b)$ で単純に指数関数的に拡大する。 これを $I_P(t\,;t_P)$ と記せば、 $$I_P(t\,;t_P) = (I_0 - J(t_P))\,e^{(a - b) t} \qquad (0 \leq t \leq t_P)$$ となる。 一方、$J(t_P) - J(t)$（上図緑色部分）は $t$ により変化し、時刻 $t$ 以後 $t_P$ までに削られた隠れた感染者に対応する部分である。 これを、 $$I_E(t\,;t_P) = (J(t_P) - J(t))\,e^{(a - b) t} \qquad (0 \leq t \leq t_P)$$ と表すものとする。 これは、$t_P$ までに判明している $J(t)$ によって求められる既知の部分となり、$I(t)$ を下から抑える。

$J(t)$ は $t$ に関して単調増加するので、$I_E(t\,;t^\prime_P)$ は $t^\prime_P$ に関して単調増加となる（すなわち、$t_{P1} \leq t_{P2} \Rightarrow$ 任意の $t < t_{P1}$ に関し $I_E(t\,; t_{P1}) \leq I_E(t\,; t_{P2})$）。 よって、特にその時点で最新となる時刻 $t_P$ の $I_E(t\,;t_P)$ が $t$ に関して最良の（最も大きな）ものとなる。

また、$I_E(t\,;t_P)$ を用い、$\dot{H}(t) = c(t) I(t), \; I_E(t\,;t_E) \geq 0$ から、検査率 $c(t)$ を上から抑える関数、 $$c_E(t\,;t_P) = \frac{\dot{H}(t)}{I_E(t\,;t_P)} \quad (\geq c(t)) \qquad (0 \leq t \leq t_P)$$ を考えることができる。

ここでは感染率 $a$ を一定のパラメーターとしているが、実際には多くの国で漸次、感染率 $a$ を減らす多大な努力が行われている。 また現時点では隠れた感染者数が十分少なくなったと見なせる国は少ない。 これらを考えるなら、ここでの $I_E(t\,;t_P)$ はよい下限を与えているとは言えない。 特に、日本のような検査を強く制限してきた国に関しては、実際の隠れた感染者数と大きな乖離が見込まれる。 一方、比較的早期に隠れた感染者を $0$ に近い値に抑え込めた韓国のような国に関しては、$I(t)$ およびそれと $H(t)$ との関係、あるいは感染初期における実際の感染率 $a$ や検査初期の隠れた感染者数 $I_0$ を考えるヒントを与えるかもしれない。 次記事において、いくつかの国に関して 2020 年 4 月 15 日時点を $t_E$ とし、倍加時間 $D = \ln 2/(a - b)$ を 1 から 9 まで変化させた $I_E(t\,;t_P)$ と $c_E(t\,;t_P)$ を求め、それらの含意について特に感染拡大初期に関し検討する。

  • [1] @barlow2001 tweet on 2020-04-23. ご精読とご指摘に感謝します。
投稿者 時刻: 0 件のコメント:

2020年4月11日土曜日

A memorandum on the observed number of infected cases

If we simply think that people randomly contact each other, and if the proportion of infected people is still small, then a) the increase in the number of infected people $I(t)$ is proportional to $I(t)$ itself. b) On the other hand, a portion of $I(t)$ is removed from $I(t)$ by healing spontaneously (or by dying without being tested). In most simple case, this can also be expressed as being proportional to $I(t)$, as seen in the classical SIR model. c) In addition, by testing for infections, people found to be infected are isolated from the population, for example, by being hospitalized. In an extreme case where a certain number of randomized tests per unit time performs, the rate of finding infected people is also proportional to $I(t)$. In another case where a certain portion of $I(t)$ becomes severe and only such patients are selectively tested (as long as the testing capacity is not saturated), confirmed cases will again be proportional to $I(t)$. Therefore, it is reasonable to think that this case is also proportional to $I(t)$. Eventually, the temporal change of $I(t)$ is $$\frac{dI}{dt} = \lambda I(t) = (a-b-c) I(t) \qquad (a, b, c > 0),$$ where $\lambda = a - b - c$, and $a$ is the rate of infection per time, $b$ is the rate of recovery, and $c$ is the rate of isolation by testing. Therefore, $I(t)$ is simply an exponential function, $$I(t) = I_0 e^{\lambda t},$$ where $I_0$ is the initial number of infected people at $t = 0$. $\lambda$ is the reciprocal of the “time constant” of the increase (i.e., the function is $e$-folded for every $1/\lambda$ of time), and when $\lambda > 0$, the function increases with time, and when $\lambda < 0$, it decreases. In the following discussion, only $a - b$ is meaningful and there is no particular need to distinguish between $a$ and $b$ in the formulas, but we use different symbols assigned to each for ease of understanding.

The number we can observe as the cumulative number of infected people is not $I(t)$ itself, but those who are removed and isolated from $I(t)$ by testing at $c I(t)$ per time. Let this be the “observed number of infected people” $H(t)$. Therefore, $$\frac{dH}{dt} = c I(t)$$ and when we put $H(0) = 0$ at $t = 0$, then $$H(t) = \frac{c I_0}{\lambda} (e^{\lambda t} - 1) = \frac{A}{\lambda}(e^{\lambda t} - 1) \qquad (\lambda \neq 0).$$ where $A = c I_0$. When $\lambda > 0$, this asymptotically approaches an exponential function at $t \rightarrow \infty$, which has the time constant $1/\lambda$ that is same as $I(t)$, and the ratio to the unobserved (hidden) infected people $I(t)$ is $I(t)/H(t) \rightarrow \lambda/c$.

Physicist Alessandro Strumia and the Financial Times journalist John Burn-Murdoch presented semi-logarithmic charts of the cumulative number of observed case by each country, aligned over time when the number reached a certain reference count[1][2]. In these plots, we can see a remarkable difference in the movements of Japan and European countries. The following is a similar plot based on data up to April 3, 2020 (data source: CSSE, Johns Hopkins University). Note that it is not the number of observed cases, but the number divided by the population of each country.

European countries such as Italy, Germany, the United Kingdom, and France have shown a similar trend, with a steep tilt (short time constant) around the reference value and then gradually slowed down in the tilt, while Japan has not seen such an initial rise and has generally remained at a constant tilt. As a result, there is great difference in the numbers of observed cases between Europe and Japan.

Let us consider to represent $H(t)$ of the model above in this plot. When $\lambda > 0$, let $t^* (> 0)$ be the time when the reference value $H^∗ (> 0)$ is reached. That is, $$H^∗ = \frac{A}{\lambda} (e^{\lambda t^∗} - 1)$$ Then, the observed number of infected persons $\tilde{H}(t)$ which is shifted so that it becomes a reference value $H^∗$ at time $t = 0$ is $$\tilde{H}(t) = \frac{A}{\lambda} (e^{\lambda (t + t^∗)} - 1) = H^∗ e^{\lambda t} + H(t)$$ Drawing $\tilde{H}(t)$ on the semi-logarithmic plot for the cases $A = 1$ and $A = 10$, assuming $H^∗ = 1$ and $\lambda = 1$, we get the following:

When we represent $\tilde{H}(t)$ in the semi-logarithmic plot as above, the slope of the plot that is proportional to the inverse of the time constant (and doubling time) is $$\frac{d}{dt}\log\tilde{H}(t) = \frac{1}{1-e^{-\lambda(t + t^*)}}\;\lambda = \frac{\lambda H^* + A}{\lambda H^* + A (1 - e^{-\lambda t})}\;\lambda \qquad (\log \mbox{is the natural logarithm}),$$ and especially at $t = 0$, we get $$\left.\frac{d}{dt}\log\tilde{H}(t)\right|_{t=0} = \frac{A\;}{H^*} + \lambda,$$ that is, the initial slope has a term proportional to $A$ in addition to $\lambda$.

The plot showed above seems to illustrate well the difference between the European countries and Japan based on actual data. That is, if there was no significant difference in the initial number of infected cases $I_0$, then the difference in the two plots was primarily due to difference in the rate $c$ of testing. The early rapid increase in Europe shows the effect of “revealing” by extensive testing, and the uniform tilt in Japan is a natural consequence of the small number of testing. In Europe, extensive testing and social distancing policies were taken, while in Japan, calls for behavioral change were made mainly by locating the attributes of clusters, so the data in the latter half of the time are influenced by them. On the other hand, the slope of the plots in the first half of the data and at some distance from the time constant $1/\lambda$ would reflect the constant $\lambda$ assumed in this model. Based on this idea, it can be seen that the speed of spread in Japan was slightly slower than in Europe[3]. However, the difference is not so much.

Again, we can largely explain the differences in the plots by difference in the amount of testing between the two, and we cannot say that there was a remarkable difference between Europe and Japan in the actual number of hidden infected persons $I(t)$ on the basis of the initial increase in Europe. And to the extent that they appear in the data, both are currently far from being successful in preventing the spread of infection.

In this memorandum, the model is kept as simple as possible for ease of analysis. A more refined model would be needed in order to analyze it in line with the actual data.

(This article is a translation of the post on April 4, 2020)

投稿者 時刻: 0 件のコメント:

2020年4月4日土曜日

観測された感染者数に関する覚書き

市中で無作為に人々が接触すると単純に考えるなら、感染者数の割合がまだ小さなとき、a) 感染者数 $I(t)$ の増加は $I(t)$ 自体に比例する。 b) 一方、$I(t)$ の一部は自然に治癒する（または検査されないまま死亡する）ことで $I(t)$ から取り除かれる。 古典的な SIR モデルに見られるように、最も単純にはこれも $I(t)$ に比例するものとして表す。 c) さらに、感染の検査が行われることで、見つかった感染者は入院するなどして人々から隔離される。 市中で無作為に時間あたり一定数の検査がなされるという極端な場合、感染者を発見する割合はやはり $I(t)$ に比例する。 他方、$I(t)$ の一定の割合が重症化し、そうした患者のみに選択的に検査がなされる場合も（検査能力が飽和しない間は）その数は $I(t)$ に比例するだろう。 よって、この場合も $I(t)$ に比例すると考えるのは妥当に見える。 このとき結局、$I(t)$ の時間変化は、 $$\frac{dI}{dt} = \lambda I(t) = (a - b - c) I(t) \quad (a, b, c > 0)$$ と表せる。 ただし、$\lambda = a - b - c$ において、$a$ は時間あたりに感染する率（感染率）、$b$ は回復率、$c$ は検査により隔離される率を表す。 よって $I(t)$ は、単純に指数関数、 $$I(t) = I_0 e^{\lambda t}$$ となる。 ただし、$I_0$ は $t = 0$ における感染者数である。 $\lambda$ は増大の「時定数」の逆数となり（すなわち、関数は時間 $1/\lambda$ ごとに $e$ 倍となり）、 $\lambda > 0$ であれば、関数は時間とともに増大し、$\lambda < 0$ であれば減少する。 なお以下の議論で、数式上、$a, b$ は特に区別する必要はなく、$a - b$ のみが意味をもつが、分かりやすさを重視し別の記号を割り当てている。

われわれが、感染者数の累計として把握できる数は $I(t)$ ではなく、検査によって $I(t)$ から時間あたり $c I(t)$ で取り除かれ隔離される人々のものである。 これを「観測された感染者数」$H(t)$ とすると、すなわち、 $$\frac{dH}{dt} = c I(t)$$ であり、$t = 0$ において $H(0) = 0$ とすれば、 $$H(t) = \frac{c I_0}{\lambda} (e^{\lambda t} - 1) = \frac{A}{\lambda} (e^{\lambda t} - 1) \qquad (\lambda \neq 0)$$ となる。 ただし、$A = c I_0$ と置いた。 $\lambda > 0$ のとき、これは、$t \rightarrow \infty$ において、$I(t)$ と同じ時定数 $1/\lambda$ を持つ指数関数に漸近し、観測されていない（隠れた）感染者 $I(t)$ との比は、$I(t)/H(t) \rightarrow \lambda/c$ となる。


われわれが知りうるのは $I$ ではなく $H$。ここでは $S$ は、十分に大きいとし、$I, H$ のみを議論している。

物理学者 Alessandro Strumia 氏および Financial Times の John Burn-Murdoch 氏は、各国の観測された累計感染者数を、感染者数がある基準値に達した時点で時間軸をそろえ片対数グラフで表した[1][2]。 このグラフに於いて、日本とヨーロッパ諸国には顕著な動きの違いが見て取れた。 以下は同様のグラフを2020年4月3日までのデータに基づいて作成したものである（データソース CSSE, Johns Hopkins University）。 ただし、観測された感染者数ではなく、各国の人口で割った値を用いている。

イタリア、ドイツ、イギリス、フランスのヨーロッパ諸国が基準値付近では急な傾き（短い時定数）を示して上昇した後、徐々に傾きを緩めていくという似た動きを示しているのに対し、日本はそのような初期の上昇がみられず概ね一定の傾きを続けている。 結果として、観測された感染者数にはヨーロッパと日本で大きな違いが生じている。

上モデルによる $H(t)$ をこのグラフで表すことを考える。 $\lambda > 0$ において、基準値 $H^* (> 0)$ に達する時刻を $t^* (> 0)$ とする。 すなわち、 $$H^* = \frac{A}{\lambda} (e^{\lambda t^*} - 1)$$ 時刻 $t = 0$ において基準値 $H^*$ となるよう時刻をずらした観測された感染者数 $\tilde{H}(t)$ は、 $$\tilde{H}(t) = \frac{A}{\lambda}(e^{\lambda (t + t^*)} - 1) = H^* e^{\lambda t} + H(t)$$ となる。 $H^* = 1, \lambda = 1$ として、$A = 1$ と $A = 10$ の場合に関して $\tilde{H}(t)$ を片対数グラフでプロットすると以下のようになる。

このように片対数グラフで $\tilde{H}(t)$ を表したとき、時定数（および倍加時間）の逆数に比例するグラフの傾きは、 $$\frac{d}{dt}\log\tilde{H}(t) = \frac{1}{1-e^{-\lambda(t + t^*)}}\;\lambda = \frac{\lambda H^* + A}{\lambda H^* + A (1 - e^{-\lambda t})}\;\lambda \qquad (\log \mbox{は自然対数})$$ となり、特に $t = 0$ での傾きは、 $$\left.\frac{d}{dt}\log\tilde{H}(t)\right|_{t=0} = \frac{A\;}{H^*} + \lambda$$ となる。 すなわち、初期の傾きには $\lambda$ の他に $A$ に比例した項が加わる。

上のグラフは、実際のデータに基づくヨーロッパと日本のプロットの違いをよく説明しているように思われる。 すなわち、初期の感染数 $I_0$ に大きな違いがなかったとすれば、両者のプロットの違いは主として検査による隔離の割合 $c$ の違いに起因したものである。 ヨーロッパの初期の急な増大は検査による「炙り出し」の効果を示し、日本のフラットな傾きは検査数の少なさによる自然な帰結である。 ヨーロッパでは広範な検査と社会的距離政策などが取られ、一方、日本では主にクラスターの属性の突き止めによる行動変容の呼びかけが行われたため、時間的に後半のデータはそれらの影響を受けている。 一方、データ前半に於いて、かつ時定数 $1/\lambda$ を単位としてある程度離れたところのプロットの傾きは、このモデルで仮定した一定の $\lambda$ を反映しているだろう。 この考えに基づけば、日本の広がりの速さはヨーロッパよりやや遅かったことが見て取れる[3]。 ただし、その違いは大きくはない。

繰り返せば、グラフの違いはほぼ両者の検査量の違いで説明でき、ヨーロッパでの初期の増加を根拠として実際の隠れた感染者 $I(t)$ の数にヨーロッパと日本とで顕著な違いがあったということはできない。 そして、データに現れる範囲で現在のところ両者とも感染の拡大防止に成功しているとは言い難い。

なおここでは解析の容易さを重視しモデルはできるだけ単純なものとした。 実際のデータに合わせて分析するためには、より精緻なモデルが必要となるだろう。

投稿者 時刻: 0 件のコメント: