市中で無作為に人々が接触すると単純に考えるなら、感染者数の割合がまだ小さなとき、a) 感染者数 $I(t)$ の増加は $I(t)$ 自体に比例する。 b) 一方、$I(t)$ の一部は自然に治癒する(または検査されないまま死亡する)ことで $I(t)$ から取り除かれる。 古典的な SIR モデルに見られるように、最も単純にはこれも $I(t)$ に比例するものとして表す。 c) さらに、感染の検査が行われることで、見つかった感染者は入院するなどして人々から隔離される。 市中で無作為に時間あたり一定数の検査がなされるという極端な場合、感染者を発見する割合はやはり $I(t)$ に比例する。 他方、$I(t)$ の一定の割合が重症化し、そうした患者のみに選択的に検査がなされる場合も(検査能力が飽和しない間は)その数は $I(t)$ に比例するだろう。 よって、この場合も $I(t)$ に比例すると考えるのは妥当に見える。 このとき結局、$I(t)$ の時間変化は、 $$\frac{dI}{dt} = \lambda I(t) = (a - b - c) I(t) \quad (a, b, c > 0)$$ と表せる。 ただし、$\lambda = a - b - c$ において、$a$ は時間あたりに感染する率(感染率)、$b$ は回復率、$c$ は検査により隔離される率を表す。 よって $I(t)$ は、単純に指数関数、 $$I(t) = I_0 e^{\lambda t}$$ となる。 ただし、$I_0$ は $t = 0$ における感染者数である。 $\lambda$ は増大の「時定数」の逆数となり(すなわち、関数は時間 $1/\lambda$ ごとに $e$ 倍となり)、 $\lambda > 0$ であれば、関数は時間とともに増大し、$\lambda < 0$ であれば減少する。 なお以下の議論で、数式上、$a, b$ は特に区別する必要はなく、$a - b$ のみが意味をもつが、分かりやすさを重視し別の記号を割り当てている。
われわれが、感染者数の累計として把握できる数は $I(t)$ ではなく、検査によって $I(t)$ から時間あたり $c I(t)$ で取り除かれ隔離される人々のものである。 これを「観測された感染者数」$H(t)$ とすると、すなわち、 $$\frac{dH}{dt} = c I(t)$$ であり、$t = 0$ において $H(0) = 0$ とすれば、 $$H(t) = \frac{c I_0}{\lambda} (e^{\lambda t} - 1) = \frac{A}{\lambda} (e^{\lambda t} - 1) \qquad (\lambda \neq 0)$$ となる。 ただし、$A = c I_0$ と置いた。 $\lambda > 0$ のとき、これは、$t \rightarrow \infty$ において、$I(t)$ と同じ時定数 $1/\lambda$ を持つ指数関数に漸近し、観測されていない(隠れた)感染者 $I(t)$ との比は、$I(t)/H(t) \rightarrow \lambda/c$ となる。
物理学者 Alessandro Strumia 氏および Financial Times の John Burn-Murdoch 氏は、各国の観測された累計感染者数を、感染者数がある基準値に達した時点で時間軸をそろえ片対数グラフで表した[1][2]。 このグラフに於いて、日本とヨーロッパ諸国には顕著な動きの違いが見て取れた。 以下は同様のグラフを2020年4月3日までのデータに基づいて作成したものである(データソース CSSE, Johns Hopkins University)。 ただし、観測された感染者数ではなく、各国の人口で割った値を用いている。
イタリア、ドイツ、イギリス、フランスのヨーロッパ諸国が基準値付近では急な傾き(短い時定数)を示して上昇した後、徐々に傾きを緩めていくという似た動きを示しているのに対し、日本はそのような初期の上昇がみられず概ね一定の傾きを続けている。 結果として、観測された感染者数にはヨーロッパと日本で大きな違いが生じている。
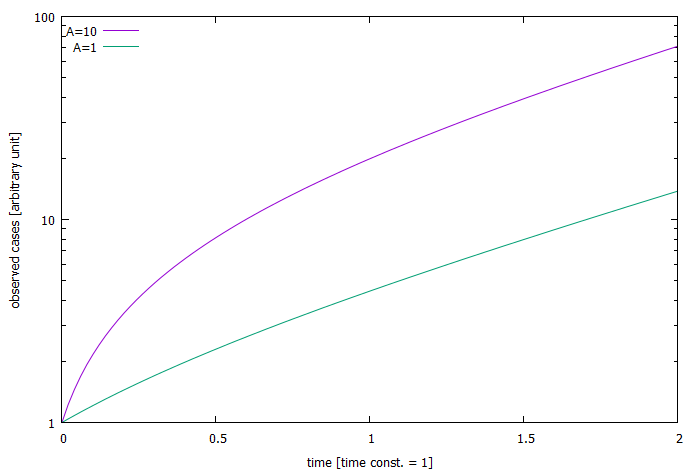
上モデルによる $H(t)$ をこのグラフで表すことを考える。 $\lambda > 0$ において、基準値 $H^* (> 0)$ に達する時刻を $t^* (> 0)$ とする。 すなわち、 $$H^* = \frac{A}{\lambda} (e^{\lambda t^*} - 1)$$ 時刻 $t = 0$ において基準値 $H^*$ となるよう時刻をずらした観測された感染者数 $\tilde{H}(t)$ は、 $$\tilde{H}(t) = \frac{A}{\lambda}(e^{\lambda (t + t^*)} - 1) = H^* e^{\lambda t} + H(t)$$ となる。 $H^* = 1, \lambda = 1$ として、$A = 1$ と $A = 10$ の場合に関して $\tilde{H}(t)$ を片対数グラフでプロットすると以下のようになる。
このように片対数グラフで $\tilde{H}(t)$ を表したとき、時定数(および倍加時間)の逆数に比例するグラフの傾きは、 $$\frac{d}{dt}\log\tilde{H}(t) = \frac{1}{1-e^{-\lambda(t + t^*)}}\;\lambda = \frac{\lambda H^* + A}{\lambda H^* + A (1 - e^{-\lambda t})}\;\lambda \qquad (\log \mbox{は自然対数})$$ となり、特に $t = 0$ での傾きは、 $$\left.\frac{d}{dt}\log\tilde{H}(t)\right|_{t=0} = \frac{A\;}{H^*} + \lambda$$ となる。 すなわち、初期の傾きには $\lambda$ の他に $A$ に比例した項が加わる。
上のグラフは、実際のデータに基づくヨーロッパと日本のプロットの違いをよく説明しているように思われる。 すなわち、初期の感染数 $I_0$ に大きな違いがなかったとすれば、両者のプロットの違いは主として検査による隔離の割合 $c$ の違いに起因したものである。 ヨーロッパの初期の急な増大は検査による「炙り出し」の効果を示し、日本のフラットな傾きは検査数の少なさによる自然な帰結である。 ヨーロッパでは広範な検査と社会的距離政策などが取られ、一方、日本では主にクラスターの属性の突き止めによる行動変容の呼びかけが行われたため、時間的に後半のデータはそれらの影響を受けている。 一方、データ前半に於いて、かつ時定数 $1/\lambda$ を単位としてある程度離れたところのプロットの傾きは、このモデルで仮定した一定の $\lambda$ を反映しているだろう。 この考えに基づけば、日本の広がりの速さはヨーロッパよりやや遅かったことが見て取れる[3]。 ただし、その違いは大きくはない。
繰り返せば、グラフの違いはほぼ両者の検査量の違いで説明でき、ヨーロッパでの初期の増加を根拠として実際の隠れた感染者 $I(t)$ の数にヨーロッパと日本とで顕著な違いがあったということはできない。 そして、データに現れる範囲で現在のところ両者とも感染の拡大防止に成功しているとは言い難い。
なおここでは解析の容易さを重視しモデルはできるだけ単純なものとした。 実際のデータに合わせて分析するためには、より精緻なモデルが必要となるだろう。
- [1] Alessandro Strumia, A tweet on 2020-03-05.
- [2] FT Visual & Data Journalism team, Coronavirus tracked: the latest figures as the pandemic spreads, Financial Times.
- [3] Yoh Tanimoto, A tweet on 2020-04-03.


0 件のコメント:
コメントを投稿